Extremwertaufgaben mit Nebenbedingung lösen
Bei Extremwertaufgaben, auch Optimierungsaufgaben oder Extremwertprobleme genannt, wird, wie der Name schon sagt, nach einem Extrempunkt gesucht. Ein Extrempunkt ist ein Hochpunkt oder ein Tiefpunkt. So kann zum Beispiel nach der größtmöglichen Fläche, die mit einem Stück Zaun eingezäunt werden kann, gefragt werden. Die Schwierigkeit bei solchen Aufgaben ist es, die passende Funktion zu bilden. Wenn du das geschafft hast, ist es ganz einfach.
Wir schauen uns nun die Vorgehensweise einmal genauer an.
Extremwertaufgaben lösen: Vorgehensweise
Als erstes liest du dir die Aufgabe genau durch und fertigst eine Skizze an. Danach gehst du folgendermaßen vor:
Methode
1. Hauptbedingung bestimmen:
Bilde zu dem Sachverhalt, der maximiert oder minimiert werden soll, die passende Funktion.
2. Nebenbedingung aufstellen:
Die gegebene Nebenbedingung muss auch in mathematischer Schreibweise notiert werden. Die Nebenbedingung ist immer eine Gleichung. In dieser Gleichung stehen vorerst immer zwei unterschiedliche Variablen, also z. B. $a$ und $b$. In einigen Fällen musst du mehrere Nebenbedingungen mathematisch ausdrücken.
3. Nebenbedingung umformen:
Forme die Nebenbedingung so um, dass eine der beiden Variablen alleine auf einer Seite der Gleichung steht.
4. Variable in Zielfunktion einsetzen:
Nun ersetzen wir in der Hauptbedingung eine Variable mit Hilfe der Nebenbedingung. Wir erhalten so eine Zielfunktion. In der Zielfunktion kommt nur noch eine Variable vor.
5. Extremwert berechnen:
Bei einer quadratischen Funktion ist der Extrempunkt immer der Scheitelpunkt. Diesen Punkt können wir mit der Formel zur Berechnung des Scheitelpunktes oder über die 1. Ableitung bestimmen. Eine andere Möglichkeit ist die quadratische Ergänzung.
6. Zweite Variable bestimmen:
Nachdem eine Variable bestimmt ist, können wir die zweite Variable ausrechnen, indem wir die bekannte Variable in die umgestellte Nebenbedingung einsetzen.
Abschließend muss nur noch die Lösung notiert werden.
Dies sieht zunächst sehr kompliziert aus. Schauen wir uns eine Extremwertaufgabe als Beispiel an, um es etwas einfacher zu machen.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Extremwertaufgaben lösen: Beispielaufgabe
Wie groß ist die größte rechteckige Fläche, die man mit einem 20 m langen Zaun einzäunen kann?
Zuerst machen wir uns eine Skizze:
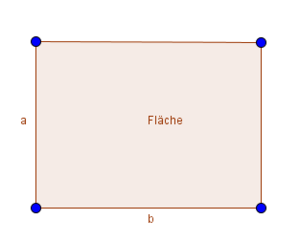
Die Fläche soll maximiert werden und der Umfang muss $20~m$ lang sein.
Vorgehensweise:
1. Hauptbedingung bestimmen
Bilde zu dem Sachverhalt, der maximiert oder minimiert werden soll, die passende Funktion.
Die Fläche soll maximiert werden. Also müssen wir hierzu die Funktion aufschreiben.
Die Formel für den Flächeninhalt eines Rechtecks lautet:
$A = a \cdot b$
2. Nebenbedingung aufstellen
Nun muss die Nebenbedingung auch in mathematischer Schreibweise notiert werden.
Unsere Nebenbedingung in dieser Aufgabe ist, dass der Zaun eine Länge von $20~m$ hat. Das bedeutet, dass der Umfang des Rechtecks $20~m$ betragen muss.
Die Formel für den Umfang eines Rechtecks lautet:
$U= 2\cdot a + 2\cdot b$
Der Umfang muss $20~m$ betragen. Wir können also $U = 20~m$ setzen.
$20~m= 2\cdot a + 2\cdot b$
3. Nebenbedingung umformen
Forme die Nebenbedingung so um, dass eine Variable alleine auf einer Seite der Gleichung steht.
Die Nebenbedingung können wir entweder nach $a$ oder nach $b$ umstellen. Wir stellen nun nach $a$ um:
$20m= 2\cdot a + 2\cdot b$ $|-2b$
$20m-2b=2a$ $| :2$
$10m-b=a$
$a=10m-b$
4. Variable in Zielfunktion einsetzen
Nun ersetzen wir in der Hauptbedingung eine Variable. Wir erhalten so die Zielfunktion. In der Zielfunktion kommt nur noch eine Variable vor.
Die Hauptbedingung lautet: $A = a \cdot b$
Wir ersetzen nun $a$ durch $10m-b$:
$A = (10m-b)\cdot b$
$A = 10m\cdot b -b^2$
5. Extremwert berechnen
Bei einer quadratischen Funktion ist das gesuchte Extremum immer im Scheitelpunkt zu finden. Diesen Punkt können wir mit der Formel zur Scheitelpunktberechnung, durch Überführen in die Scheitelpunktform (über die quadratische Ergänzung) oder über die 1. Ableitung bestimmen.
Wir werden hier die quadratische Ergänzung anwenden. Klicke auf den Link, falls du dir die quadratische Ergänzung noch einmal anschauen möchtest.
$A = 10m\cdot b -b^2$
$A = -b^2+10m\cdot b$
Als erstes müssen wir den Faktor, der vor dem $b^2$ steht, ausklammern (hier: $-1$):
$A = -b^2+10m\cdot b$
$A = -(b^2-10m\cdot b)$
Nun muss die Zahl, die vor dem b steht (hier: $10~m$), zunächst durch 2 dividiert werden und das Ergebnis dann quadriert werden. Dieser Wert wird dann einmal addiert und einmal subtrahiert:
$A = -(b^2-10m\cdot b)$
$A = -(b^2-10m\cdot b+25m^2-25m^2)$
Der negative Wert, der nicht für die binomische Formel benötigt wird, muss ausgeklammert werden:
$A = -(b^2-10m\cdot b+25m^2)-(-25m^2)$
Jetzt können wir die binomische Formel anwenden:
$A = -(b-5m)^2+25m^2$
Abschließend können wir nun den Scheitelpunkt ablesen:
$S(5/25)$
Merke
$f(x) = a\cdot(x−d)^2+e$
Scheitelpunkt: S $(d/e)$
Wenn $b= 5~m$ ist, dann beträgt der Flächeninhalt des Rechtecks $25~m^2$. Dies ist der größte Flächeninhalt, der möglich ist, wenn der Umfang $20~m$ betragen muss.
6. Zweite Variable bestimmen
Nachdem die erste Variable bestimmt ist, können wir die zweite Variable mithilfe der umgestellten Nebenbedingung ganz einfach berechnen.
$a=10m-b$
$a= 10m-5m$
$a=5m$
Das Ergebnis können wir überprüfen, indem wir $a$ und $b$ in die Hauptbedingung einsetzen:
$A=a\cdot b = 5m \cdot 5m = 25 m^2$
Dies stimmt mit unserem Scheitelpunkt überein.
Lösung: Wenn man mit einem $20~m$ langen Zaun eine möglichst große rechteckige Fläche einzäunen möchte, dann müssen die Seitenlängen des Rechtecks jeweils $5~m$ lang sein. Die Fläche des Rechtecks (bzw. Quadrats) ist dann maximal und beträgt $25~m^2$.
Teste dein neu erworbenes Wissen zu Extremwertaufgaben mit Nebenbedingung an unseren Übungen. Wir wünschen Dir dabei viel Spaß und Erfolg!
Teste dein Wissen!
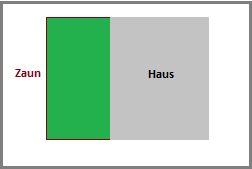
Es soll ein Gehege für vier Kaninchen geschaffen werden. Es wird empfohlen für jedes Kaninchen $5m^2$ einzuplanen. Es stehen insgesamt $11m$ Zaun zur Verfügung. Der Zaun soll an dem Haus befestigt werden, um so ein rechteckiges Freilaufgehege für die vier Kaninchen zu schaffen.
Reicht der Zaun aus, um den Kaninchen genügend Auslauf zu geben?
Es ist eine Funktion gegeben, die die Stückkosten einer Firma beschreibt. Die Stückkosten sollen nun auf den minimalen Wert gebracht werden. Welcher mathematische Punkt der Funktion wird gesucht?
Auf einem Campingplatz in den Niederlanden bekommt jeder Zelter ein 40m langes Seil. Mit diesem Seil soll er seinen Zeltplatz abgrenzen. Der Campingplatz ist, außer am Eingang, vollständig von einer Hecke umgeben. Die Zeltplätze, die direkt an die Hecke angrenzen, müssen dort nicht mit dem Seil abgegrenzt werden.
Wie viel Platz haben die Zelter, die in einer Ecke zelten, die Zelter, die an einer Heckenwand zelten und die Zelter, die in der Mitte des Campingplatzes zelten?
(Hinweis: Die Zeltplätze müssen rechteckig (bzw. quadratisch) sein.)
Markiere die richtige Antwort.
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema





























































