Lineares Wachstum und lineare Abnahme
In diesem Text erklären wir dir, was lineares Wachstum bzw. lineare Abnahme ist und was du damit berechnen kannst. Du findest hier auch je ein Zahlenbeispiel zu den beiden Themen.
Definition
Es gibt verschiedene Arten von Wachstum und Zerfall. Das lineare Wachstum und die lineare Abnahme haben eine konstante Änderungsrate. Das bedeutet, dass in gleichen Abständen die gleiche Menge dazu kommt oder weggenommen wird. Daraus ergibt sich, dass der Funktionsgraph eine Gerade ist.
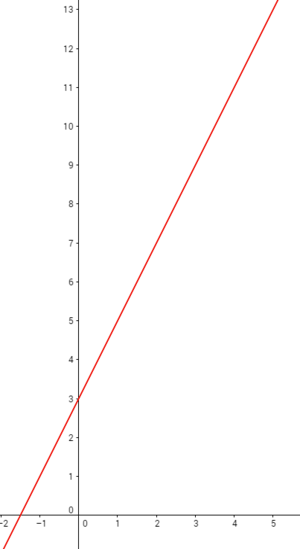
Abbildung: lineares Wachstum
Die Funktionsgleichung ist allgemein:
Methode
$N(t) = N_0 + a\cdot t$
Dabei ist:
| $N(t)$: | Wert zum Zeitpunkt $t$ |
| $N_0$: | Anfangswert zum Zeitpunkt $t=0$ |
| $a$: | Änderungsrate |
| $t$: | Variable, meist Zeit |
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Lineares Wachstum
Ein Beispiel für lineares Wachstum ist das gleichmäßige Befüllen eines Gefäßes.
Die Änderungsrate muss beim linearen Wachstum positiv sein:
$ a>0$
Der Anfangswert $N_0$ wächst pro Zeiteinheit um den Wert der Änderungsrate $a$. Das sieht man weiter oben in der Grafik. Wenn zum Beispiel der Anfangswert $N_0 = 3$ beträgt und mit jeder Zeiteinheit $a = 1,75$ dazu kommen, dann lautet eine mögliche Gleichung: $N(t) = N_0 + a \cdot t = 3 + 1,75 \cdot t$
Schauen wir uns ein Beispiel an:
Beispiel
Ein Schwimmbecken wird mit Wasser gefüllt. Am Anfang ist das Becken leer. Pro Minute laufen nun $20~l$ Wasser in das Becken. Das Schwimmbecken fasst insgesamt $54.000~l$.
Fragen:
1. Wie viel Wasser befindet sich nach einer Stunde in dem Becken?
2. Nach welcher Zeit ist das Becken vollständig mit Wasser gefüllt?
Antworten:
Als erstes müssen wir die Funktionsgleichung aufstellen:
$N(t) = 0 + 20 \cdot t $
Dabei ist $t$ die Zeit in Minuten und $N(t)$ die Wassermenge in Litern.
Mit dieser Gleichung kann nun die Wassermenge zu jedem beliebigen Zeitpunkt berechnet werden. Mit dieser Gleichung kann auch berechnet werden, wie lange es dauert, bis eine bestimmte Wassermenge in dem Becken ist.
1. $N(60) = 20 \cdot 60 = 1200$
Nach $60$ Minuten sind $1.200~ l$ Wasser in dem Schwimmbecken.
2. $N(t) $ muss $54.000~l$ betragen:
$54000 = 20 \cdot t $
$t =\frac{54000}{20} = 2700~min$
Nach $2.700$ Minuten (45 Stunden) ist das Becken vollständig mit Wasser gefüllt.
Lineare Abnahme
Bei der linearen Abnahme sinkt der Wert konstant. Als Beispiel könnte man das gleichmäßige Abfließen von Wasser aus einer Badewanne nennen.
Die Änderungsrate bei der linearen Abnahme muss negativ sein.
Von dem Anfangswert $N_0$ wird dann $t$-mal der Wert von $a$ abgezogen.
Schauen wir uns ein Beispiel an:
Beispiel
Anka hat $50$ € zu Weihnachten geschenkt bekommen. Sie liebt Rosinenschnecken und kauft sich daher von dem Geld jede Woche eine. Eine Rosinenschnecke kostet $2$ €.
Fragen:
1. Nach wie vielen Monaten ist das Geld aufgebraucht?
2. Wie viel Geld ist nach acht Wochen noch übrig?
Antworten:
Wir müssen als erstes die Gleichung für den Sachverhalt aufstellen. Der Anfangswert beträgt $50$ € und die Änderungsrate ist $-2$ € je Woche:
$N(t) = 50 -2 \cdot t$
Dabei ist $t$ die Zeit und wird in Wochen angegeben und $N(t)$ ist der Geldbetrag in Euro.
1. Wenn das Geld aufgebraucht ist, gilt: $N(t) = 0$
Wir ersetzen also $N(t)$ durch $0$ und formen die Gleichung dann nach $t$ um:
$0 = 50 - 2\cdot t$
$t = \frac{-50}{-2} = 25$
Nach $25$ Wochen, also nach ca. $6$ Monaten, ist das Geld aufgebraucht.
2. Um den Geldbetrag nach acht Wochen zu ermitteln, müssen wir für $t$ den Wert $8$ einsetzen:
$N(8) = 50 - 2\cdot 8 = 34 $
Nach acht Wochen sind noch $34$ € übrig.
In den Übungsaufgaben kannst du dich prüfen. Viel Erfolg dabei!
Video: Simon Wirth
Text: Chantal Rölle
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Urheber: Simon Wirth, Fabian Serwitzki, Frank Kreuzinger, selbständiger Diplompädagoge, Pirna (Lektorat, fachliche Textkorrekturen und Grafikerstellung)
Teste dein Wissen!
Klaus hat zu Weihnachten 30 € von seinen Großeltern bekommen. Er hat sich vorgenommen das Geld zu sparen und jeden Monat weitere 5 € in seine Spardose zu werfen. Welche Funktionsgleichung beschreibt den Sachverhalt?
Hans und seine Familie machen Urlaub auf Ibiza. Sie buchen einen Leihwagen. Die Grundgebühr beträgt 25 € und der Preis pro gefahrenem Kilometer beträgt 0,50 €, inklusive Sprit.
Hans hat für das Auto 100 € eingeplant. Nun fragt er sich, wie viele Kilometer er damit fahren kann. Kannst du ihm helfen?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
