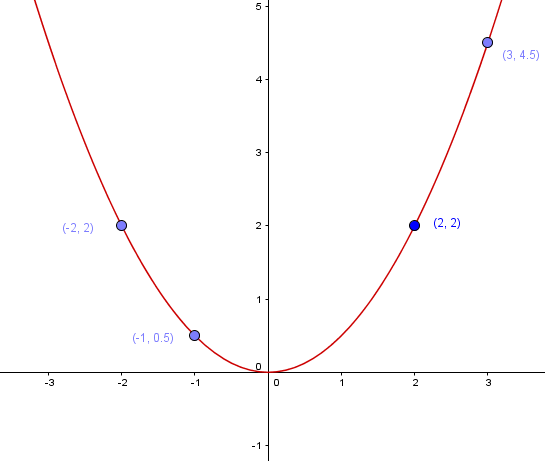
Streckung und Stauchung einer Normalparabel
Thema des folgenden Lerntextes ist das Stauchen und Strecken von Parabeln in der Mathematik. Wir klären die Bedeutung des Faktors $a$, welcher vor dem $x^2$ in einer Funktion steht. Er wird auch Streckfaktor genannt und kann eine Funktion strecken oder stauchen (bzw. an der x-Achse spiegeln (die Funktion $_"$umdrehen$"$)). Wir behandeln hier Funktionen, deren Bilder Parabeln sind. Unsere Aussagen über den Streckfaktor vergleichen die entstehende Funktion immer mit $f(x)=x^2$.
Stauchen und Strecken von Parabeln: 6 Fakten
Im Folgenden geben wir dir vorab schonmal einen groben Überblick über das, was du über Streckung und Stauchung wissen musst:
Methode
Methode
Hier klicken zum Ausklappen
Wenn $a$ eine beliebige reelle Zahl (außer $0$) ist, dann gelten für $f(x)=ax^2$:
- Der Faktor $a$ gibt an, wie eine Funktion gestreckt oder gestaucht wurde.
- Wenn $a$ größer als $1$ oder kleiner als $-1$ ist, dann ist die Funktion gestreckt.
- Wenn $a$ zwischen $1$ und $-1$ liegt, dann ist die Funktion gestaucht.
- Ist $a=1$ oder $a=-1$, dann ist der Graph von $f$ eine Normalparabel oder eine umgekehrte Normalparabel.
- Ist der Streckfaktor größer als Null, dann ist der Funktionsgraph nach oben geöffnet.
- Ist der Streckfaktor kleiner als Null, dann ist der Funktionsgraph nach unten geöffnet.
Wir erklären dir nachfolgend die oben genannten Kurzinformationen. Zusätzlich gehen wir mit dir eine Übung durch, damit du fit im Thema Stauchung und Streckung von Normalparabeln wirst.
Definition des Streckfaktors
Merke
Merke
Hier klicken zum Ausklappen
Sowohl bei der allgemeinen Form als auch bei der Scheitelpunktform ist der Streckfaktor $a$ die reelle Zahl (außer $0$), die sich als Faktor auf $x$ in seiner quadratischen Form bezieht, zum Beispiel $f(x)=\textcolor{red}{3}x^2+1$ oder $f(x)=\textcolor{red}{0,5}(x-2)^2-4$.
$\textcolor{red}a>1$ oder $\textcolor{red}a<-1$: (Betrag von $a$ größer als $1$) $\rightarrow$ Funktion gestreckt
$-1<\textcolor{red}a<1$: (Betrag von $a$ kleiner als $1$) $\rightarrow$ Funktion gestaucht
Allgemeine Form: $f(x)=\textcolor{red}a⋅x^2+b⋅x+c$
Scheitelpunktform:$f(x)=\textcolor{red}a⋅(x−d)^2+e$
Öffnung nach oben und nach unten
Der Graph ist nach oben geöffnet, wenn a positiv ist. Der Graph ist nach unten geöffnet, wenn a negativ ist. Du musst also bei Parabeln nicht berechnen, sondern nur ablesen, in welche Richtung sie geöffnet sind.
Merke
Merke
Hier klicken zum Ausklappen
$a>0$ (a größer als 0, a ist positiv) $\rightarrow $ der Graph ist nach oben geöffnet
$a<0$ (a kleiner als 0, a ist negativ) $\rightarrow $ der Graph ist nach unten geöffnet
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Streckung einer Parabel
Wenn der Faktor vor dem $x^2$ größer als $1$ oder kleiner als $-1$ ist, wird die Funktion gestreckt. Dies kann man sich relativ einfach erklären: Die Normalparabel hat den Streckfaktor $1$ ($f(x) = x^2$); daraus ergeben sich folgende Punkte, die auf der Normalparabel liegen:
$1^2 = 1$ $\rightarrow $ P(1/1)
$2^2 = 4$ $\rightarrow $ Q(2/4)
$3^2 = 9$ $\rightarrow $ R(3/9)
Jede Quadratzahl wird nun mit $a$ multipliziert.
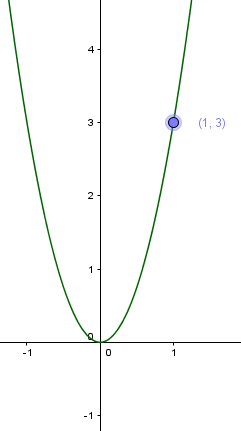
Nehmen wir an, der Faktor vor dem $x^2$ beträgt $3$. Dann wird jede Quadratzahl mit $3$ multipliziert. In diese Funktion $f(x) = 3·x^2$ setzen wir nun die ersten x-Werte ein:
$3 · 1^2 = 3 · 1 = 3$ $\rightarrow $ P(1/3)
$3 · 2^2 = 3 · 4 = 12$ $\rightarrow $ P(2/12)
$3 · 3^2 = 3 · 9 = 27$ $\rightarrow $ P(3/27)
Dabei musst du darauf achten, dass immer zuerst die Quadratzahl ausgerechnet wird. Danach wird die Quadratzahl mit $a$ multipliziert, nicht umgekehrt!
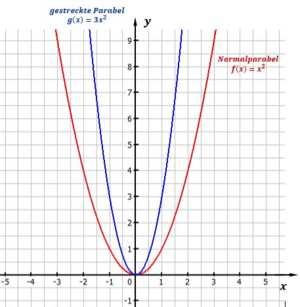
Abbildung: zwei quadratische Funktionen
Die linke Funktion ist um den Faktor $3$ gestreckt, die rechte Funktion ist die Normalparabel. Siehst du den Unterschied?
Wie du siehst, ist die linke Funktion nach $_"$oben gezogen$"$ (gestreckt).
Stauchung einer Parabel
Wenn wir als Faktor vor dem $x^2$ eine Zahl stehen haben, die zwischen $-1$ und $1$ liegt, wird die Funktion gestaucht oder anders gesagt $_"$zusammengedrückt$"$.
Wenn wir nun eine Zahl vor dem $x^2$ stehen haben, werden die Quadratzahlen mit diesem Wert multipliziert.
Nehmen wir an, der Faktor vor dem $x^2$ beträgt $0,2$. Dann wird jede Quadratzahl mit $0,2$ multipliziert.
In diese Funktion $f(x) = 0,2·x^2$ setzen wir nun die ersten x-Werte ein:
$0,2 · 1^2 = 0,2 · 1 = 0,2$ $\rightarrow $ P(1/0,2)
$0,2 · 2^2 = 0,2 · 4 = 0,8$ $\rightarrow $ P(2/0,8)
$0,2 · 3^2 = 0,2 · 9 = 1,8$ $\rightarrow $ P(3/1,8)
Wie du siehst, steigt der Graph weniger steil als bei der Normalparabel und sieht so aus:
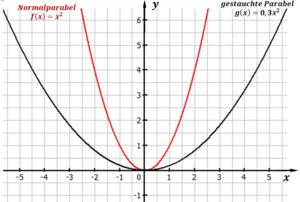
Die Funktion sieht so aus, als hätte sie jemand zusammengedrückt (gestaucht).
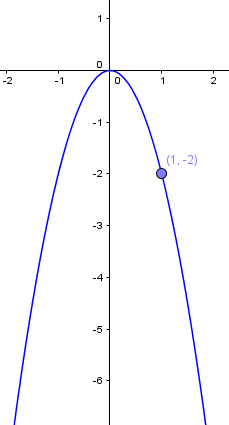
Quadratische Funktionen nach unten geöffnet
Eine Funktion ist nach unten geöffnet, wenn der Faktor vor dem $x^2$ negativ ist. Denn wenn wir vor das $x^2$ einen negativen Faktor setzen, werden die y-Werte negativ.
Hierzu nun ein Beispiel: Wir schauen uns die Funktion $f(x) = -x^2$ an und erstellen für die Funktion eine Wertetabelle.
| x-Werte | y-Werte |
|---|---|
| -1 | f(-1)= -(-1)² = -1 |
| 0 | 0 |
| 1 | f(1) = - (1)² = -1 |
| 2 | -4 |
| 3 | -9 |
Versuche, mithilfe der Wertetabelle die Normalparabel zu zeichnen.
Gut zu wissen
Hinweis
Hier klicken zum Ausklappen
Möchtest du noch einmal vertiefen, wie du eine Normalparabel zeichnen kannst? Im Lerntext Quadratische Funktionen zeichnen, erklären wir dir dies ausführlich.
Diese umgedrehte Normalparabel kann nun wieder gestreckt oder gestaucht werden.
Hierzu ein letztes Beispiel:
$f(x) = - 0,9 x^2 + 3$
Die Funktion ist gestaucht und nach unten geöffnet, da der Faktor zwischen $-1$ und $1$ liegt und negativ ist. Außerdem wird wegen $+3$ in der Funktionsgleichung um $3$ nach oben verschoben. Und somit sieht der Graph so aus:
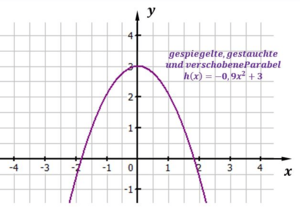
Jetzt weißt du auch schon, wie eine Funktion gestreckt und gestaucht wird. Außerdem hast du gelernt, wann eine quadratische Funktion nach oben oder unten geöffnet ist.
Gut zu wissen
Hinweis
Hier klicken zum Ausklappen
Im Lerntext Wie verschiebt man eine Normalparabel kannst du nachlesen und lernen, wie du eine Normalparabel verschiebst. Außerdem lernst du dort, wie du an einer Funktion erkennst, um wie viele Stellen und in welche Richtung diese Funktion verschoben wurde.
Überprüfe dein Verständnis zur Streckung und Stauchung von Normalparabeln mit unseren Übungsaufgaben. Wir wünschen dir dabei viel Spaß!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Lektor: Frank Kreuzinger
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
