Kosinusfunktion und ihre Eigenschaften
In diesem Lerntext erhältst du einen Überblick über die Eigenschaften der Kosinusfunktion. Außerdem erklären wir dir, wie du die Kosinuskurve in x- oder y-Richtung verschieben kannst.
Allgemeine Funktionsgleichung
Die Kosinusfunktion ist eine der trigonometrischen Funktionen und ordnet jedem $x$ seinen entsprechenden Kosinuswert $y$ zu.
Zu sehen ist ein Einheitskreis. Der heißt so, weil die Länge seines Radius‘ 1 beträgt.
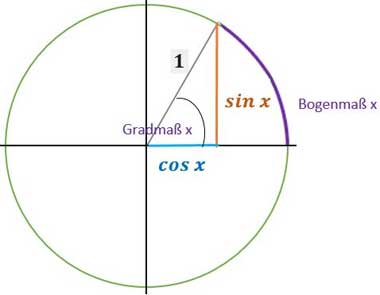
Die Kosinusfunktion ordnet jedem Winkel eine Streckenlänge zu. Die Länge der blau gezeichneten Strecke gehört dabei zu dem Winkel $x$. Ist $x$ zum Beispiel mit $60°$ gegeben, so ist die Länge der blauen Strecke $0,5$. Daher ist cos $60°=0,5$. Zu jedem Winkel gehört eine Länge des Kreisbogens. Der ist hier lila als Bogen eingezeichnet. Die Länge dieses Bogens nennt man auch Bogenmaß des Winkels $x$. Ist der Radius 1, dann ist der Umfang des gesamten Kreises $U = \pi \cdot d = \pi \cdot 2r = \pi \cdot 2 \cdot 1 = 2\pi $. Der gesamte Kreis hat also eine Bogenlänge von $2π$. Das sind ca. $6,28$ Einheiten (zum Beispiel cm). Also gehört zum Winkel $360°$ das Bogenmaß $2π$. Entsprechend gehört zum Gradmaß $60°$ das Bogenmaß $ \frac{2\pi}{6} = \frac{\pi}{3}$.
Merke
$y~= cos(x)$
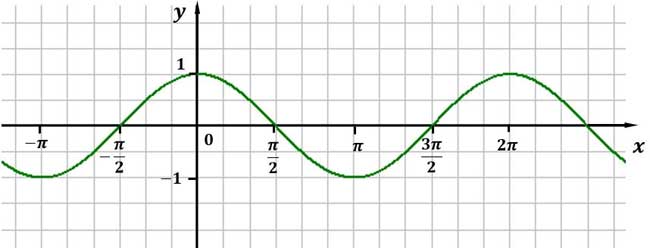
Die Kosinusfunktion mit der x-Achse im Bogenmaß.
Die Kosinusfunktion hat, genau wie die Sinusfunktion einige Besonderheiten. Für die Skalierung der Achse wird in der Regel das Bogenmaß genutzt. Wichtig ist an der Stelle, ob der Taschenrechner mit dem Gradmaß oder dem Bogenmaß rechnen soll. Das muss in den Einstellungen berücksichtigt werden. In der Regel gibt es auf dem Taschenrechner die Einstellungen RAD (für Bogenmaß) und DEG (für Gradmaß).
Definitions- und Wertemenge der Kosinusfunktion
Für die x-Werte der Kosinusfunktion sind alle reellen Zahlen erlaubt. Die Definitionsmenge lautet also:
$\mathbb{D} = \mathbb{R}$
Wie du in der Abbildung erkennen kannst können die y-Werte nur Werte von $-1$ bis $1$ annehmen. Der Wertebereich der normalen Kosinusfunktion lautet also:
$W= [-1;1]$
Periode und Symmetrieverhalten der Kosinuskurve
Die Kosinuskurve verläuft periodisch, das heißt, dass sich ein einzelner Abschnitt immer wieder wiederholt. Man kann auch sagen, dass sich die Funktionswerte $y$ im selben Abstand wiederholen. Eine Wellenbewegung oberhalb und unterhalb der x-Achse entspricht einer kleinsten Periode von $2 \pi$.
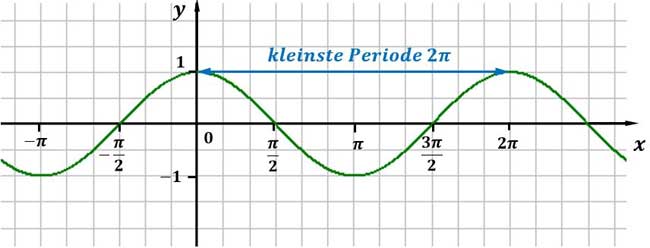
Außerdem ist die Kosinusfunktion achsensymmetrisch zur y-Achse. Dies lässt sich rechnerisch beweisen:
$cos(-x) = cos (x)$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Nullstellen der Kosinusfunktion
Die Kosinusfunktion besitzt unendlich viele Nullstellen. Diese Nullstellen liegen jeweils um den Wert $\pi$ auseinander. Das sieht man in der unteren Grafik.
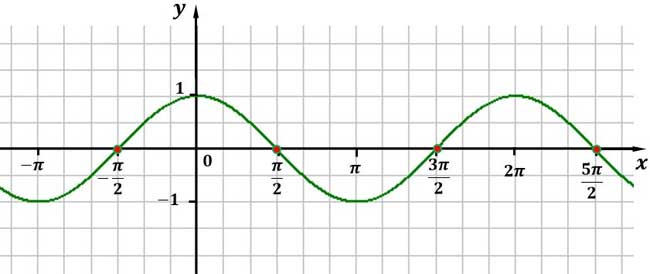
Nullstellen der Kosinusfunktion
Merke
Für die Berechnung der Nullstellen der Kosinusfunktion gilt:
$x_k = \frac{\pi}{2} + k \cdot \pi $
Dabei können für $k$ alle möglichen ganzen Zahlen eingesetzt werden.
Beispiel
$x_{-1} = \frac{\pi}{2} + (-1) \cdot \pi = - \frac{\pi}{2}$
$x_{0} = \frac{\pi}{2} + 0 \cdot \pi = \frac{\pi}{2}$
$x_{3} = \frac{\pi}{2} + 2 \cdot \pi = \frac{5 \cdot \pi}{2}$
Relative Maxima und Minima
Auch für die Extremwerte (Hoch- und Tiefpunkte) lässt sich aufgrund des periodischen Verlaufs der Kosinuskurve eine allgemeine Formel angeben.
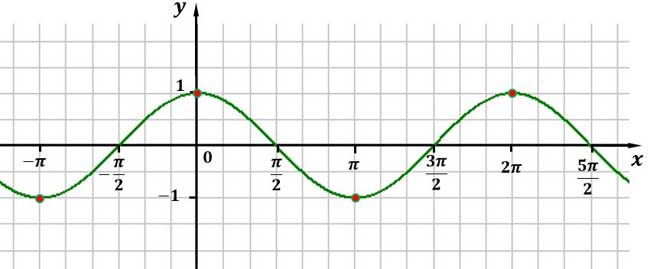
Extrempunkte der Kosinusfunktion
Merke
Relative Maxima liegen für jede ganze Zahl k bei:
$x_k = k \cdot 2 \cdot \pi$
Beispiel
$x_{-1} = -1 \cdot 2 \cdot \pi = -2 \cdot \pi$
$x_1 = 1 \cdot 2 \cdot \pi = 2 \cdot \pi$
Merke
Relative Minima liegen für jede ganze Zahl k bei:
$x_k = \pi + k \cdot 2 \cdot \pi$
Beispiel
$x_{-1} = \pi + k \cdot 2 \cdot \pi = \pi + (-1) \cdot 2 \cdot \pi = - \pi$
$x_{1} = \pi + 1 \cdot 2 \cdot \pi = 3 \cdot \pi$
Verschiebung in y-Richtung
Die Kosinusfunktion wird entlang der y-Achse verschoben, wenn ein Wert zum Funktionsterm dazu addiert oder davon abgezogen wird. Dadurch wird die Kosinuskurve entlang der y-Achse in positive oder negative Richtung verschoben.
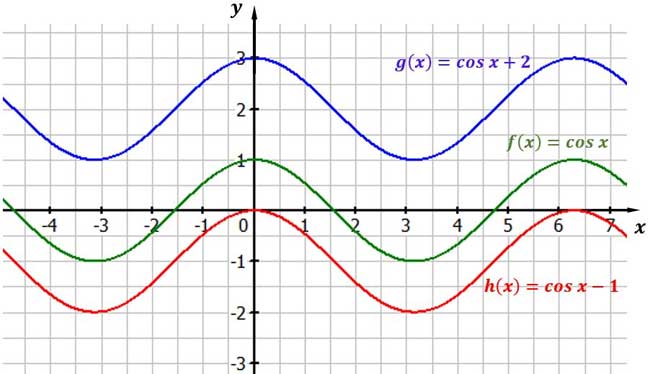
Verschiedene Funktionen der Form $f(x)=cos x+d$
Merke
$y = cos(x) + d$
Der Parameter $d$ verschiebt die Kosinuskurve entlang der y-Achse.
$d>0 \rightarrow$ Verschiebung nach oben
Die x-Koordinaten der Maxima und Minima ändern sich nicht.
Verschiebung in x-Richtung
Außerdem kann die Kosinuskurve entlang der x-Achse verschoben werden.
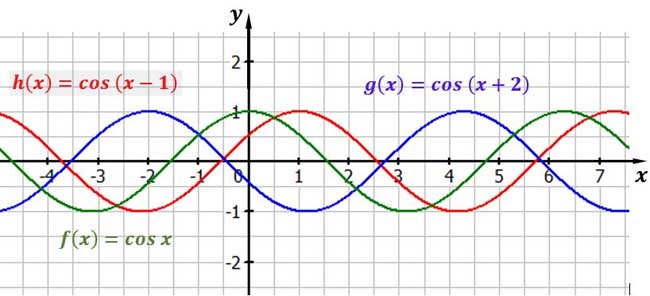
Verschiebung der Kosinuskurve entlang der x-Achse
Merke
$y = cos(x + c)$
Der Parameter $c$ verschiebt die Kosinusfunktion entlang der x-Achse.
$c>0 \rightarrow$ Verschiebung nach links
Bei der Verschiebung entlang der x-Achse ändern sich sowohl Null- als auch Extremstellen der Funktion.
Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben! Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Urheber: Simon Wirth, Fabian Serwitzki, Frank Kreuzinger
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
