Wie verschiebt man eine Normalparabel?
Der Graph der Funktion $f(x)=x^2$ wird Normalparabel genannt. Der Graph dieser Funktion kann in einem Koordinatensystem in 4 verschiedene Richtungen verschoben werden: Nach oben, nach unten, nach links und nach rechts.
Übersicht
Merke
Für beliebige positive reelle Zahlen $a$, $b$, $c$ und $d$ gilt:
Verschiebung in Richtung der y-Achse
nach $\textcolor{red}{oben}$ : $f(x) = x^2 \textcolor{red}{+ a} \rightarrow$ Verschiebung des Graphen um a nach oben
nach $\textcolor{red}{unten} $ : $f(x) = x^2 \textcolor{red}{-b} \rightarrow$ Verschiebung des Graphen um b nach unten
Verschiebung in Richtung der x-Achse
nach $\textcolor{red}{rechts} $ : $f(x) = (x \textcolor{red}{-c})^2 \rightarrow$ Verschiebung des Graphen um c nach rechts
nach $\textcolor{red}{links} $ : $f(x) = (x \textcolor{red}{+d})^2 \rightarrow$ Verschiebung des Graphen um d nach links
Verschiebung nach oben
Die Normalparabel wird nach oben verschoben, indem zu $x^2$ eine positive Zahl addiert wird. Der Graph von $g(x)=x^2+10$ ist gegenüber dem Graphen von $f(x)=x^2$ um $10$ Einheiten nach oben verschoben.
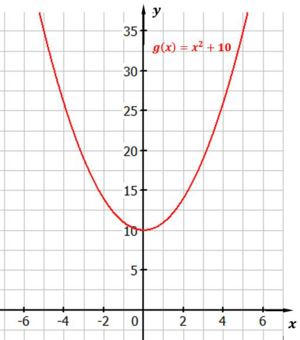
Abbildung: Normalparabel um $10$ nach oben verschoben
Die Normalparabel wurde um $10$ Einheiten in Richtung der y-Achse nach oben verschoben.
Verschiebung nach unten
Die Normalparabel wird nach unten verschoben, indem zu $x^2$ ein negativer Wert addiert wird. Der Graph von $g(x)=x^2-3$ ist gegenüber dem Graphen von $f(x)=x^2$ um $3$ Einheiten nach unten verschoben.
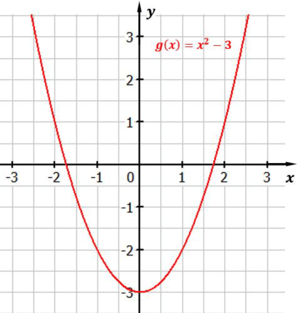
Abbildung: Normalparabel um $3$ nach unten verschoben
Die Normalparabel wurde um $3$ Einheiten in Richtung der y-Achse nach unten verschoben.
Verschiebung nach rechts
Der Graph der Normalparabel wird nach rechts verschoben, indem von $x$ eine positive Zahl subtrahiert wird und die Differenz dann quadriert wird.
Das ist zum Beispiel $f(x)=(x-3)^2$
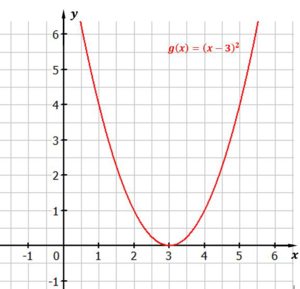
Abbildung: Normalparabel um $3$ nach rechts verschoben
Also bewirkt der negative Wert, der mit dem $x$ in der Klammer steht, dass die Parabel auf der x-Achse nach rechts, also in den positiven Bereich verschoben wird.
Merke dir einfach: Wenn die Zahl, die dem $x$ in der Klammer folgt, negativ ist, dann wird die Parabel nach rechts, also in den positiven Bereich verschoben.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Verschiebung nach links
Hier ist es genau umgekehrt im Vergleich zur Verschiebung nach rechts: Der Graph der Normalparabel wird nach links verschoben, indem zu $x$ eine positive Zahl addiert wird und die Summe dann quadriert wird.
Das ist zum Beispiel: $f(x) = (x+5)^2$
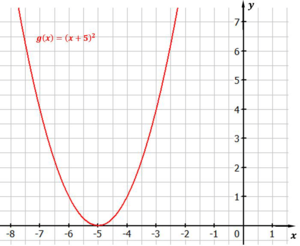
Abbildung: Normalparabel um $5$ nach links verschoben
Also bewirkt der positive Wert, der mit dem $x$ in der Klammer steht, dass die Parabel auf der x-Achse nach links, also in den negativen Bereich verschoben wird.
Merke dir einfach: Wenn die Zahl, die dem $x$ in der Klammer folgt, positiv ist, dann wird die Parabel nach links, also in den negativen Bereich verschoben.
Beides zusammen
Natürlich können wir den Graphen zum Beispiel auch nach unten und gleichzeitig nach rechts verschieben.
Sagen wir der Graph soll um $3$ nach unten und um $1$ nach rechts verschoben werden. Wie muss unsere Funktion dann aussehen?
Vertiefung
Lösung
Wir gehen schrittweise vor:
Zuerst verschieben wir den Graphen um $3$ nach unten $\rightarrow f(x) = x^2-3$.
Dann noch um $1$ nach rechts $\rightarrow f(x) = (x-1)^2-3$.
Jetzt haben wir unseren Graphen und der sieht gezeichnet so aus:
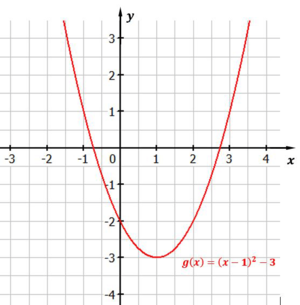
Abbildung: Normalparabel um $3$ nach unten und um $1$ nach rechts verschoben
Die Funktion kann auch in Normalform angegeben werden. Leider können wir daraus die Verschiebung nicht direkt ablesen. Schauen wir uns ein Beispiel an. $f(x) = x^2+2x+5$. Der Graph dazu sieht so aus:
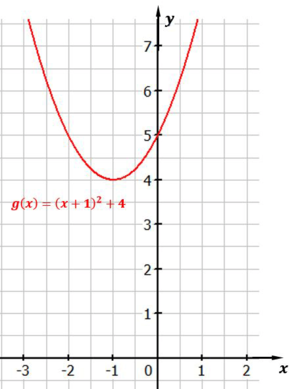
Abbildung: Normalparabel um $1$ nach links und um $4$ nach oben verschoben
Das einzige, was wir aus der Funktion direkt ablesen können, ist der y-Achsenabschnitt, also hier $5$.
Nun können wir die Form natürlich in die Scheitelpunktform umformen.
$f(x) = x^2+2x+5$
$f(x) = (x^2+2x+1-1)+5$
$f(x) = (x^2+2x+1)+5-1$
$f(x) = (x+1)^2+4$
Jetzt können wir die Verschiebung ablesen. Der Graph wird um 1 nach links verschoben und um 4 nach oben. Wir können dies nun nochmal mit dem Bild von oben vergleichen; das Bild bestätigt, dass der Scheitelpunkt der Funktion bei S(-1/4) liegt.
Jetzt hast du einen Überblick über die verschiedenen Verschiebungen der Normalparabel bekommen. Dieses Wissen kannst du gerne an unseren Übungen testen. Wir wünschen dir viel Spaß dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Lektor: Frank Kreuzinger
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
