Potenzfunktionen: Umkehrfunktion aufstellen leicht erklärt
In diesem Text erklären wir dir, was die Umkehrfunktion einer Potenzfunktion ist und wie du sie berechnen kannst.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Definition
Hier erfährst du, was eine Umkehrfunktion ist und wie du eine Umkehrfunktion berechnen kannst.
Umkehrfunktion
Umkehrfunktionen ordnen, wie der Name schon sagt, die Variablen umgekehrt zu. Das bedeutet, dass der $x$-Wert mit dem $y$-Wert getauscht wird. Dies ist nur möglich, wenn es für jeden Funktionswert $(y)$ nur einen $x$-Wert gibt. Grafisch kannst du die Umkehrfunktion bilden, indem du die Funktion an der Winkelhalbierenden, also an der Funktion $g(x) =x$, spiegelst.
Die Umkehrfunktion der Funktion $f(x)$ wird mit $f^{\textcolor{red}{-1}} (x)$ gekennzeichnet. Die hochgestellte $\textcolor{red}{-1}$ ist also das Zeichen für die Umkehrfunktion.
Um eine Umkehrfunktion zu bilden, muss die Funktion zunächst nach $x$ umgestellt werden. Danach werden $x$ und $y$ getauscht, dabei vertauscht sich auch die Definitions- und die Wertemenge.
Methode
Vorgehensweise: Umkehrfunktion bilden
Die Funktion nach $x$ auflösen.$x$ und $y$ tauschen.
Schauen wir uns zwei Beispiele an:
Beispiel
Hier klicken zum Ausklappen$y = 3x^2+5$
Hier müssen wir den Definitionsbereich einschränken, da das Bild eine quadratische Parabel ist, die nicht eindeutig ist.
Die Parabel hat ihren Scheitelpunkt auf der $y$-Achse. Damit ist sie zum Beispiel für $x ≥ 0$ umkehrbar. Dieser Parabelast ist eindeutig. Der Definitionsbereich für diese Funktion seien also alle reellen Zahlen, die größer oder gleich Null sind. Den Wertebereich bilden alle reellen $y$-Werte die größer oder gleich 5 sind, denn die Parabel ist nach oben offen und ihr Scheitelpunkt liegt bei 5 auf der $y$-Achse.
Definitionsbereich: D$f$:$x$ ∈ ℝ, $x$ ≥0
Wertebereich: W$f$:$y$ ∈ ℝ, $y$ ≥5
1. Die Funktion nach $x$ auflösen.
$y = 3x^2+5~~~~~~~~~~~~~~~~~~~~~~|-5$
$y-5 = 3x^2~~~~~~~~~~~~~~~~~~~~~~~|:3$
$\frac{y-5}{3}=x^2~~~~~~~~~~~~~~~~~|\sqrt{~~}$
$\sqrt{\frac{y-5}{3}}=x$
2. $x$ und $y$ tauschen.
$\sqrt{\frac{x-5}{3}}=y$ bzw. $y= \sqrt{\frac{x-5}{3}}$
Beispiel
Wir bilden hier die Umkehrfunktion für $x$ ≥ 0.
Das Beispiel gibt es für den gesamten Definitionsbereich auf Wie bildet man eine Umkehrfunktion?
$f(x)= 5x^3$
1. Die Funktion nach $x$ auflösen.
$y =5x^3~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~|:5$
$\frac{y~}{5~}=x^3~~~~~~~~~~~~~~~~~~~~~~~~~~~|\sqrt[3]{~~}$
$\sqrt[3]{\frac{y~}{5~}}=x$
2. $x$ und $y$ tauschen.
$f^{-1}(x) = \sqrt[3~]{\frac{x~}{5~}}$
Potenzfunktion
Gut zu wissen
Hinweis
Für jede ganze Zahl n ist $f(x) = x ^\textcolor {red}{n}$ eine Potenzfunktion.
Potenzfunktion mit positivem Exponenten verlaufen immer durch den Ursprung. In diesem Text schauen wir uns aber nur die Umkehrfunktionen von solchen Potenzfunktionen an.
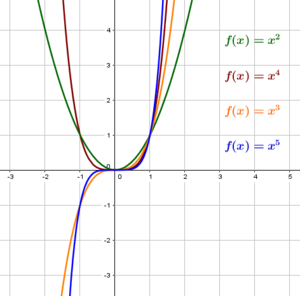
Abbildung: Graphen von Potenzfunktionen mit natürlichen Exponenten
Wie sehen die Umkehrfunktionen von solchen Potenzfunktionen mit positiven Exponenten aus?
Umkehrfunktionen von Potenzfunktionen
Die Umkehrfunktion der Potenzfunktion $f(x) = x^3$ soll gebildet werden. Wir gehen so vor, wie oben beschrieben:
Beispiel
Auch hier bilden wir die Umkehrfunktion für x≥0. Wir schränken hier den Definitionsbereich ein, da Wurzelfunktionen für negative Werte nicht erklärt sind.
1. Die Funktion nach $x$ auflösen:
$y = x^3 ~~~~~~~|\sqrt[3]{~~}$
$\sqrt[3]{y}= x$
2. $x$ und $y$ tauschen:
Abbildung: Funktion $f(x) = x^3 $ und die Umkehrfunktion $f^{-1}(x)= \sqrt[3]{x}$
Bei allen anderen Potenzfunktionen, die einen ungeraden Exponenten haben, kann man genauso vorgehen. Bei Potenzfunktionen, die einen geraden Exponenten haben, muss man anders verfahren, denn jedem $y$-Wert außer dem vom Scheitelpunkt, werden zwei $x$-Werte zugeordnet. So ist beispielsweise bei der Funktion $y=x^2$ für den $y$-Wert $y= 4$ sowohl $x=2$ als auch $x=-2$ richtig. Daher muss der Definitionsbereich eingeschränkt werden.
Schauen wir uns dazu die Umkehrfunktion der Funktion $f(x)=x^2$ an:
Beispiel
Es muss zunächst die Definitionsmenge festgelegt werden. Wir wollen die Umkehrfunktion für alle positiven $x$-Werte bilden, $x\ge 0$.
1. Die Funktion nach $x$ auflösen:
$f(x)= x^2 ~~~~~~~|\sqrt[2]{~~}$
$\sqrt[2]{y}= x$
2. $x$ und $y$ tauschen:
$f^{-1}(x)= \sqrt[2]{x} =\sqrt{x}$, für alle $x\ge 0$.
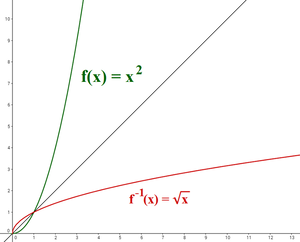
Abbildung: Funktion $f(x) = x^2 $ mit Umkehrfunktion $f^{-1}(x)= \sqrt[2]{x}$
Mit den Aufgaben kannst du dein neu erworbenes Wissen überprüfen. Viel Erfolg dabei!
Video: Simon Wirth
Text: Chantal Rölle
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Lektor: Frank Kreuzinger
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
