Übersicht: Funktionstypen und ihre Eigenschaften
Es gibt eine Vielzahl an verschiedenen Funktionsarten. Hier erhältst du eine Übersicht über die Funktionstypen, die in der Schule besprochen werden.
Die Einteilung in Funktionsarten bietet eine Hilfe, da gleiche Funktionsarten oft ähnliche Eigenschaften und Merkmale besitzen.
Übersicht der Funktionen
Hier erhältst du eine kurze Übersicht zu den Funktionen in Mathe.
Merke
- Potenzfunktionen: $f(x) = a\cdot x^{n}$
1. Fall: gerader, positiver Exponent
2. Fall: ungerader, positiver Exponent
3. Fall: gerader, negativer Exponent
4. Fall: ungerader, negativer Exponent - Ganzrationale Funktionen: $f(x) = a x^n + b x^{n-1} + ...$ Sonderformen: Lineare Funktionen, Quadratische Funktionen
- Exponentialfunktion: $f(x) = a^{~x}$
- Logarithmusfunktionen
- Trigonometrische Funktionen Sinus, Kosinus und Tangens
- Weitere Funktionen: Umkehrfunktionen der trigonometrischen Funktionen, hyperbolische Funktionen und deren Umkehrfunktionen (Areafunktionen)
Noch nicht alles klar? Du hast jetzt eine kleine Übersicht über die mathematischen Funktionen erhalten. Wir möchten dir nun alles etwas detaillierter erklären, damit du fit in diesem Thema wirst. Falls dir das noch nicht genügt, gelangst du über die obigen Begriffe zu den jeweiligen Seiten.
Potenzfunktionen
Merke
Potenzfunktionen nennt man alle Funktionen der Form: $f(x) = a\cdot x^{n}$, wobei $a$ und $n$ beliebige reelle Zahlen sind.
Im Folgenden betrachten wir Potenzfunktionen mit ganzem Exponenten. Je nachdem welche Zahl der Exponent ist, ergibt sich eine andere Funktion. Hierbei werden vier verschiedene Fälle unterschieden:
1. Fall: gerader, positiver Exponent
Merke
Gerade und positive Exponenten
Die Funktionen besitzen immer die Punkte $P_1(-1|1)$, $S(0|0)$, $P_2(1|1)$.
Die einzige Nullstelle liegt im Ursprung.
Der Definitionsbereich umfasst alle reellen Zahlen, also D = ℝ.
Der Wertebereich ist W = [0; ∞[
Der Graph ist achsensymmetrisch zur Y-Achse.
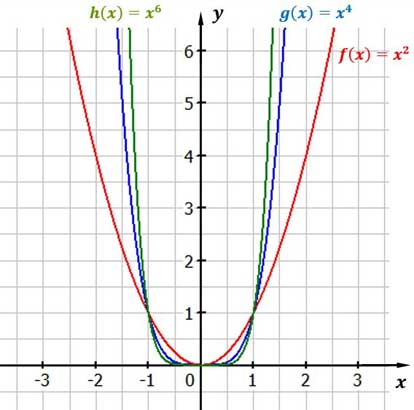
Potenzfunktionen mit geradem, positiven Exponenten
2. Fall: ungerader, positiver Exponent
Merke
Ungerade und positive Exponenten
Die Grenzwerte streben für x 0 +∞.
Die Funktionen haben diese Punkte gemeinsam: $P_1(-1|-1)$, $S(0|0)$, $P_2(1|1)$.
Die einzige Nullstelle liegt im Ursprung.
Der Definitionsbereich und der Wertebereich sind D = W = ℝ.
Die Funktionen sind punktsymmetrisch zum Ursprung.
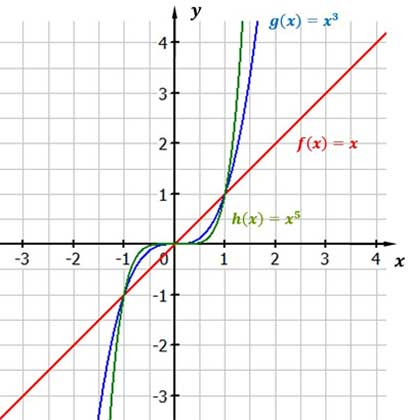
Potenzfunktionen mit ungeradem, positiven Exponenten
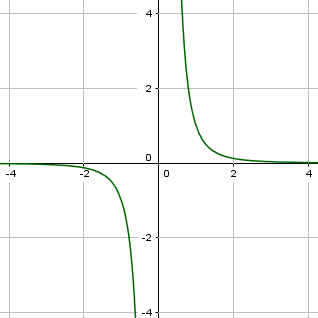
3. Fall: gerader, negativer Exponent
Merke
Gerader und negativer Exponent
Die Grenzwerte sind dann wie folgt:
Wenn x den Wert 0 anstrebt (der Wert geht also immer näher an die Zahl Null), streben die y-Werte +∞ an.
Wenn x den Wert -|+ ∞ anstrebt, streben die y-Werte 0 an.
Die Funktionen haben diese Punkte gemeinsam: $P_1(-1|1)$, $P_2(1|1)$.
Es gibt keine Nullstelle.
Der Definitionsbereich ist D = ℝ\{0}.
Der Wertebereich ist W = ]0; ∞[. Das sind alle positiven reellen Zahlen.
Die Funktionen sind alle achsensymmetrisch zur y-Achse.
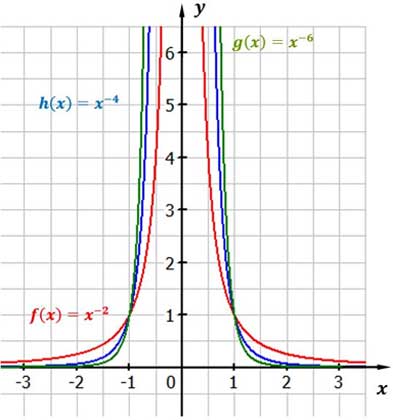
Potenzfunktionen mit geradem, negativen Exponenten
4. Fall: ungerader, negativer Exponent
Merke
Ungerade und negative Exponenten
Die Grenzwerte sind wie folgt:
Sowohl die x- als auch die y-Achse sind Asymptoten.
Die Funktionen haben diese Punkte gemeinsam: $P_1(-1|-1)$, $P_2(1|1)$.
Es gibt keine Nullstellen.
Der Definitionsbereich und der Wertebereich sind D = W = ℝ\{0}.
Die Funktionen sind punktsymmetrisch zum Ursprung.
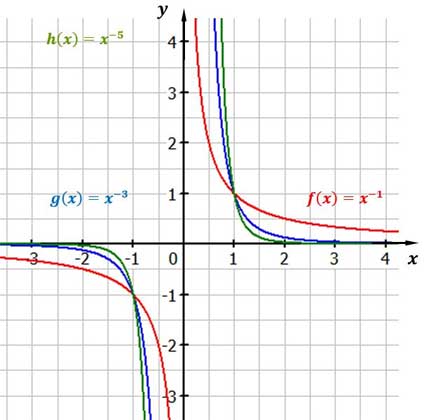
Potenzfunktionen mit ungeradem, negativen Exponenten
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Ganzrationale Funktionen bestimmen
Merke
Ganzrationale Funktionen sind Funktionen der Form: $f (x)$ = $a$ n $x$ n + $a$n-1$x$ n-1 + ... + $a$ 2 $x$ 2 + $a$ 1$x$ + $a$0
"wobei $a$ n, $a$ n-1, ..., $a$1, $a$0 reelle Zahlen sind und $a$n nicht Null ist und $n$ eine beliebige natürliche Zahl ist."
Funktionen, bei denen $n=1$ ist, heißen lineare Funktionen ( $f(x)$ = $a$1$x$ + $a$0 ).
Funktionen, bei denen $n=2$ ist, heißen quadratische Funktionen ( $f(x)$ = $a$2$x$2 + $a$1$x$ + $a$0 ).
Die Buchstaben vor den Potenzen werden oft anders benannt, so wie hier bei uns im weiteren Text.
Ganzrationale Funktionen: Lineare Funktionen
Das Bild von linearen Funktionen ist eine Gerade, wie du in der nächsten Grafik sehen kannst. Das bedeutet, dass die Steigung in jedem Punkt gleich ist. Das Anstiegsdreieck, das du in der Abbildung siehst, könntest du auch entlang der Funktion verschieben.
Merke
$f(x) = \textcolor{red}{m}\cdot x + \textcolor{blue}{n}$
$\textcolor{red}{m: Steigung}$
$\textcolor{blue}{n: y-Achsenabschnitt}$
$x:$ unabhängige Variable
$f(x) = y:$ abhängige Variable
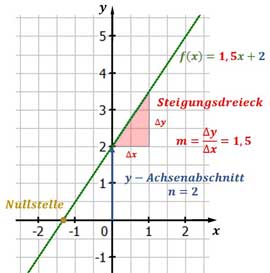
Abbildung einer linearen Funktion mit y-Achsenabschnitt, Nullstelle und Steigungsdreieck
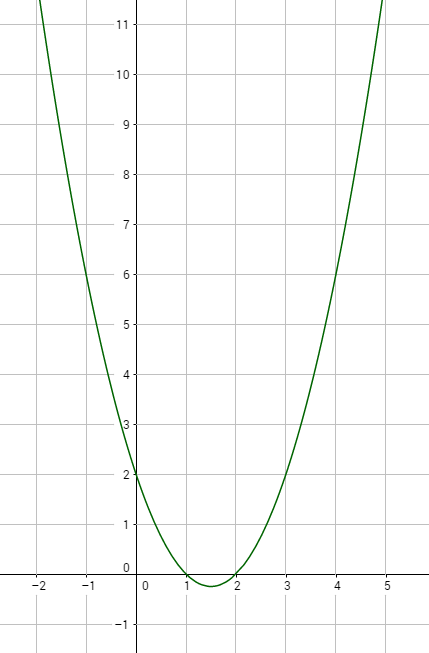
Ganzrationale Funktionen: Quadratische Funktionen
Bei quadratischen Funktionen wird das $x$ zum Quadrat genommen: $\rightarrow f(x) = ax^2+bx+c$
Es ergibt sich die Form einer Parabel:
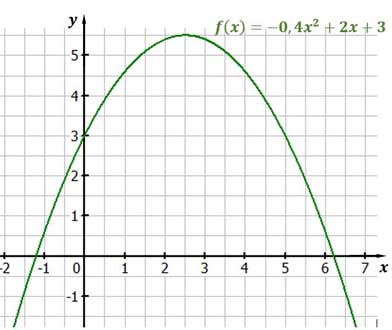
Außer beim Scheitelpunkt gibt es zu jedem y-Wert zwei x-Werte.
Quadratische Funktionen können sowohl in der Normalform als auch in der Scheitelpunktform angegeben sein:
Gut zu wissen
Hinweis
Allgemeine Form: $f(x) = \textcolor{red}{a} \cdot {x^2} + {b} \cdot {x} +c$
Scheitelpunktform: $f(x) = \textcolor{red}a\cdot(x−\textcolor{blue}d)^2+\textcolor{green}e$
Streckungsfaktor: $\textcolor{red}a$
Scheitelpunkt: S $(\textcolor{blue}d/\textcolor{green}e)$
Die beiden Formen kann man gegenseitig ineinander umformen.
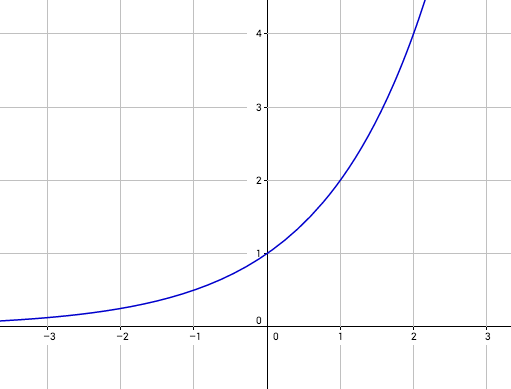
Exponentialfunktionen
Bei Exponentialfunktionen steht die Variable im Exponenten.
Merke
Eine Funktion der Form $f(x) = a^{~x}$ nennt man Exponentialfunktion. Dabei ist $a$ eine positive reelle Zahl.
Den Definitionsbereich bilden alle relle Zahlen ($D$ = ℝ). Der Wertebereich ist die Menge aller positiven reellen Zahlen ($W$ = ]0 ❘ ∞[ ).
Ist $a$ eine Zahl zwischen Null und Eins, so ist die Funktion streng monoton fallend, ist $a$ größer als Eins, so ist die Funktion streng monoton wachsend. Die x-Achse ist stets Asymptote. Der Punkt (0 ❘ 1) ist gemeinsamer Punkt all dieser Funktionen.
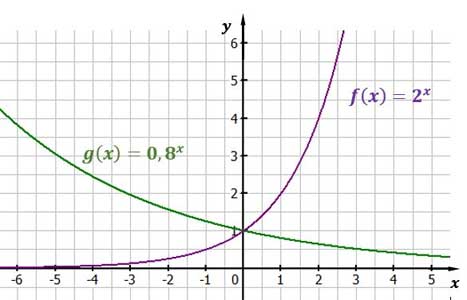
Abbildung: Exponentialfunktion
Logarithmusfunktionen
Exponentialfunktionen und Logarithmusfunktionen sind Umkehrfunktionen voneinander.
Merke
Eine Funktion der Form $f(x)=log_ax$ nennt man ELogarithmusfunktion. Dabei ist $a$ eine positive reelle Zahl.
Den Definitionsbereich bilden alle positive reellen x-Werte (D=]0|∞[). Der Wertebereich ist die Menge aller reellen Zahlen (W=R).
Ist $a$ eine Zahl zwischen Null und Eins, so ist die Funktion streng monoton fallend, ist a größer als Eins, so ist die Funktion streng monoton wachsend. Die y-Achse ist stets Asymptote. Der Punkt P(1|0) ist gemeinsamer Punkt aller dieser Funktionen.
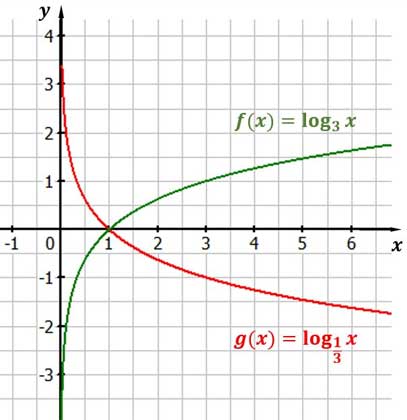
Trigonometrische Funktionen Sinus, Kosinus und Tangens
Sinus, Kosinus und Tangens sind trigonometrische Funktionen (Winkelfunktionen) mit denen du Berechnungen in einem Dreieck durchführen kannst. Wir beschränken uns hier wieder auf die Angabe einiger Eigenschaften.
Merke
Sinus
Definitionsbereich: D=R oder: alle reellen x
Wertebereich: $W=[-1|1]$ oder: $-1≤y≤1$
Nullstellen:$x_k=kπ$
Maxima bei: $x_k= \frac{π}{2}+2kπ$
Minima bei: $x_k= \frac{3π}{2}+2kπ$
kleinste Periode: $2π$
$k$ ist jeweils eine beliebige ganze Zahl
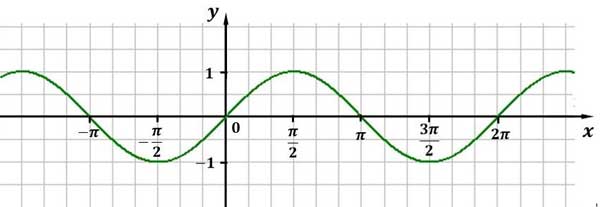
Abbildung: Graph der Sinusfunktion
Kosinus
Definitionsbereich: D=R oder: alle reellen x
Wertebereich: $W=[-1|1]$ oder: $-1≤y≤1$
Nullstellen:$x_k= \frac{π}{2}+kπ$
Maxima bei: $x_k= 2kπ$
Minima bei: $x_k= π+2kπ$
kleinste Periode: $2π$
$k$ ist jeweils eine beliebige ganze Zahl
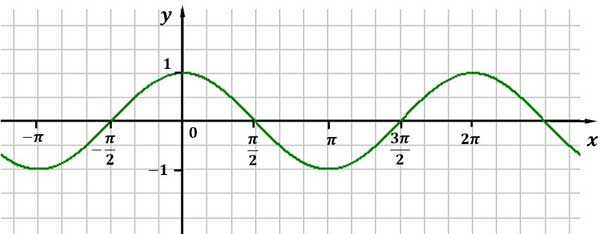
Abbildung: Graph der Kosinusfunktion
Tangens
Definitionsbereich: D=R,x≠ \frac{π}{2}+kπ
Wertebereich: $W=R$ oder: alle reellen $y$
Nullstellen:$x_k=kπ$
Senkrechte Asymptoten/Polgeraden: $x_k= \frac{π}{2}+kπ$
kleinste Periode: $π$
$k$ ist jeweils eine beliebige ganze Zahl
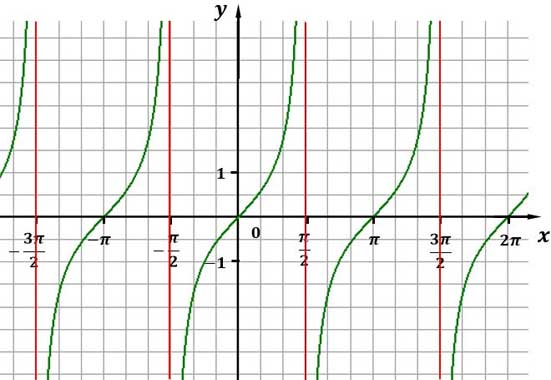
Abbildung: Graph der Tangensfunktion
Nun hast du eine Übersicht über die mathematischen Funktionen erhalten. Du kannst dein Wissen mit unseren Übungsaufgaben zu ganzrationalen Funktionen und anderen Funktionen testen. Viel Erfolg dabei!
Video: Fabian Serwitzki
Text: Chantal Rölle
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Urheber: Simon Wirth, Fabian Serwitzki, Frank Kreuzinger
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
