Nullstellen berechnen mit der p-q-Formel - so geht's!
Bei vielen Aufgaben, die dir zum Thema quadratische Gleichungen gestellt werden, sollst du die Nullstellen berechnen.
Suchst du jetzt einen Nullstellenrechner? Du willst ganz bequem mit einem pq-Formel-Rechner online deine Mathematikaufgabe lösen? Dann bist du hier falsch. Wir erklären dir aber dafür in wenigen Schritten, wie du ganz ohne Online-Rechner Nullstellen mit der p-q-Formel berechnest. Werde jetzt Profi in der Nullstellenberechnung!
Was sind Nullstellen?
Nullstellen sind diejenigen x-Werte, die eingesetzt in die Funktionsgleichung $f(x)$, null ergeben. Im Falle der quadratischen Funktion sind die Nullstellen die Stellen, an denen der Graph der Funktion $f(x)$ die x-Achse schneidet.
Merke
Merke
Hier klicken zum Ausklappen
$f(x) = a \cdot x^2 + b\cdot x + c = 0 $
Im Falle der quadratischen Funktion sind dies genau die x-Werte, an der der Graph die x-Achse schneidet. Der Wert der y-Koordinate muss also $0$ sein.
In Bezug auf die Anzahl der Nullstellen gibt es drei verschiedene Möglichkeiten:
- Zwei Nullstellen
- Genau eine Nullstelle
- Keine Nullstelle
Im Folgenden beschäftigen wir uns mit diesen verschiedenen Möglichkeiten und bestimmen die jeweiligen Nullstellen mithilfe der p-q-Formel.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Quadratische Funktionen mit zwei Nullstellen
Unser wichtigstes Werkzeug, um die Nullstellen bestimmen zu können, ist die p-q-Formel, die du wahrscheinlich schon beim Lösen quadratischer Gleichungen eingesetzt hast. Mithilfe dieser Formel lassen sich quadratische Gleichungen, die in der Normalform stehen, durch direktes Einsetzen lösen.
Merke
Merke
Hier klicken zum Ausklappen
p-q-Formel
$x_{1/2} = -\frac{\textcolor{red}{p}}{2}\pm \sqrt{(\frac{\textcolor{red}{p}}{2})^2-\textcolor{green}{q}}$
Bestimmung von p und von q:
$f(x) = x^2+{\textcolor{red}{ p}} \cdot x +{\textcolor{green}{ q}} = 0$
Wichtig ist dabei, dass der Faktor vor dem $x^2$ gleich 1 ist. Ist dies nicht der Fall, musst du die Gleichung so umstellen, dass sich der Faktor 1 ergibt. Dies machst du, indem du die ganze Gleichung durch den Faktor vor $x^2$ teilst. Hierzu ein Beispiel:
Beispiel
Beispiel
Hier klicken zum Ausklappen
$f(x) = 3\cdot x^2+6\cdot x-4$
1. Quadratische Gleichung umformen
$0 = 3\cdot x^2+6\cdot x-4$ $|:3$
Zuerst müssen wir durch 3 teilen, damit der Faktor vor dem $x^2$ gleich 1 ist.
$0 = x^2+2\cdot x-\frac{4}{3}$
Nun haben wir die Funktion so umgestellt, dass wir p und q bestimmen können.
2. Bestimmung von p und q
$0 = x^2+\textcolor{red}{2}\cdot x \textcolor{green}{-\frac{4}{3}}$
$0 = x^2+{\textcolor{red}{ p}} \cdot x +{\textcolor{green}{ q}} = 0$
- $\textcolor{red}{p=2}$
- $\textcolor{green}{q=-\frac{4}{3}}$
Setzen wir diese Werte nun in die p-q-Formel ein und berechnen $x$.
3. p-q-Formel anwenden
$x_{1/2} = -\frac{2}{2}\pm \sqrt{(\frac{2}{2})^2-(-\frac{4}{3})}$
$x_{1/2} = -\frac{2}{2}\pm \sqrt{\frac{2^2}{4}-(-\frac{4}{3})}$
$x_{1/2} = -1\pm \sqrt{1+\frac{4}{3}}$
$x_1 = -1 + \sqrt{1+\frac{4}{3}} \approx 0,53$
$x_2 = -1 - \sqrt{1+\frac{4}{3}} \approx -2,53$
Charakteristisch für quadratische Funktionen mit zwei Nullstellen ist, dass unter der Wurzel eine positive Zahl steht. Daraus ergeben sich zwei Werte für x( $x_1, x_2$). Dies lässt sich vor allem mit der p-q-Formel gut nachvollziehen, da wir einmal plus und einmal minus den Wert der Wurzel rechnen.
$\rightarrow x_{1/2} = -\frac{p}{2}\textcolor{red}{\pm}\sqrt{\frac{p^2}{4}-q}$.
Betrachten wir noch ein weiteres Beispiel.
Beispiel
Beispiel
Hier klicken zum Ausklappen
$f(x) = -x^2+10\cdot x+16$
$0 = -x^2+10\cdot x+16 = 0$ $|\cdot (-1)$
Wir multiplizieren zunächst mit $-1$, damit der Faktor vor $x^2$ gleich $1$ ist.
$0 = x^2 - 10\cdot x-16$
Nun können wir die Werte für p und q aus der Gleichung ablesen:
- $ p= - 10$
- $ q= -16$
$x_{1/2} = -\frac{-10}{2}\pm \sqrt{(\frac{-10}{2})^2-(-16)}$
$x_{1/2} = 5\pm \sqrt{\frac{100}{4}+16}$
$x_{1/2} = 5\pm \sqrt{25+16} = 5\pm \sqrt{41}$
$x_1 = 5 + \sqrt{41} \approx 11,4$
$x_2 = 5 - \sqrt{41} \approx -1,4 $
Charakteristisch für die Funktionen mit zwei Nullstellen, ist, dass unter der Wurzel eine positive Zahl steht. Daraus ergeben sich dann zwei Werte ($x_1, x_2$), da wir einmal plus und einmal minus den Wert der Wurzel rechnen. $\rightarrow x_{1/2} = -\frac{p}{2}\textcolor{red}{\pm}\sqrt{\frac{p^2}{4}-q}$.
Quadratische Funktionen mit einer Nullstelle
Quadratische Funktionen, die nur genau eine Nullstelle haben, berühren die x-Achse in einem Punkt. Man sagt dazu auch, dass der Graph die x-Achse tangiert.
Schauen wir uns ein Beispiel an:
Beispiel
Beispiel
Hier klicken zum Ausklappen
1. Quadratische Funktion gleich null setzen
$f(x) = x^2 - 8\cdot x + 16$
$0 = x^2 - 8\cdot x + 16$
2. Bestimmung von p und q
- $ p= - 8$
- $ q= 16$
3. p-q-Formel anwenden
$x_{1/2} = -\frac{-8}{2}\pm \sqrt{(\frac{-8}{2})^2-(16)}$
$x_{1/2} = -\frac{-8}{2}\pm \sqrt{\frac{-8^2}{4}-(16)}$
$x_{1/2} = 4\pm \sqrt{\frac{64}{4}-16}$
$x_{1/2} = 4\pm \sqrt{16-16} = 4\pm \sqrt{0}$
$x_1 = 4 + 0 = 4$
$x_2 = 4 - 0 = 4$
Beim Berechnen der Nullstelle mithilfe der p-q-Formel solcher Funktionen, erkennen wir sofort eine Besonderheit: Bei der Anwendung der p-q-Formel ergibt der Wert unterhalb der Wurzel immer null. Aus diesem Grund kommen keine unterschiedlichen Ergebnisse für $x_1$ und $x_2$ heraus und wir erhalten lediglich genau eine Nullstelle.
Quadratische Funktionen ohne Nullstelle
Wie kann es sein, dass eine quadratische Funktion keine Nullstelle besitzt?
Betrachten wir beispielsweise die Funktion $f(x) = x^2 - 4\cdot x + 5$. Wir erkennen, dass der Graph die x-Achse weder schneidet noch berührt. Er besitzt also keine Nullstelle.
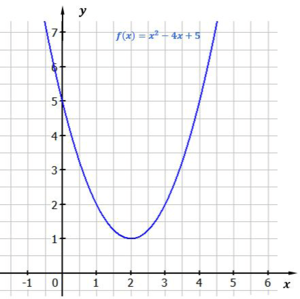
Welches Ergebnis erhalten wir aber, wenn wir versuchen, die Nullstellen der Funktion mithilfe der p-q-Formel zu berechnen?
Beispiel
Beispiel
Hier klicken zum Ausklappen
1. Quadratische Gleichung gleich null setzen
$f(x) = x^2-4x+5$
$0 = x^2-4x+5$
2. Bestimmung von p und q
- $p= -4$
- $q= 5$
3. p-q-Formel anwenden
$x_{1/2} = -\frac{-4}{2}\pm \sqrt{(\frac{-4}{2})^2-(5)}$
$x_{1/2} = 2\pm \sqrt{\frac{16}{4}-5}$
$x_{1/2} = 2\pm \sqrt{4-5}$
$x_{1/2} = 2\pm \sqrt{-1}$
$\textcolor{red}{\sqrt{-1}}\rightarrow$ im Bereich der reellen Zahlen nicht berechenbar.
Da die p-q-Formel nicht lösbar ist, gibt es kein Ergebnis und somit auch keine reellen Nullstellen.
Anzahl der Nullstellen aus der p-q-Formel ablesen
Merke
Merke
Hier klicken zum Ausklappen
Zwei Nullstellen
Der Wert unter der Wurzel in der p-q-Formel ist positiv.
Genau eine Nullstelle
Der Wert unter der Wurzel ist genau null.
Keine Nullstelle
Der Wert unter der Wurzel ist negativ.
Beispielaufgabe - Nullstellen berechnen
Schauen wir uns diese Funktionen an, die zwei Schnittpunkte mit der x-Achse und somit auch zwei Nullstellen hat.
$f(x) = 4 x^2 +12 x + 6$
Versuche die Nullstellen einmal selber mithilfe der p-q-Formel zu berechnen.
Vertiefung
Hier klicken zum Ausklappen
Lösung
1. Quadratische Gleichung umformen
$f(x) = 4 x^2 +12 x + 6$
$0 = 4 x^2 +12 x + 6$ $|:4$
$0 = x^2 +3 x + 1,5$
2. Bestimmung von p und q
$p=3$
$q=1,5$
3. p-q-Formel anwenden
$x_{1/2} = -\frac{3}{2}\pm \sqrt{(\frac{3}{2})^2-1,5}$
$x_{1/2} = -1,5\pm \sqrt{\frac{9}{4}-1,5}$
$x_{1/2} = -1,5\pm \sqrt{0,75}$
$x_1 = -1,5 + \sqrt{0,75} \approx -0,63$
$x_2 = 5 - \sqrt{41} \approx -2,36 $
Jetzt kannst du die Nullstellen von quadratischen Funktionen mithilfe der pq-Formel berechnen. Teste dein neu erlerntes Wissen jetzt mithilfe unserer Übungen. Viel Spaß und Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Lektor: Frank Kreuzinger
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
Jetzt registrieren und kostenlose Probestunde anfordern.
Dein Gratis-Lernpaket:
- Nachhilfe-Probestunden gratis
- Hausaufgaben-Soforthilfe: 15 Gratis-Minuten
- Lern-Bibliothek: 1 Tag Gratis-Zugang