Merke
- $f(x) = 2 \cdot e^{2x}$
- $f´(x) = 2 \cdot 2\cdot e^{2x}$$=4 \cdot e^{2x}$
- $f´´(x) = 2 \cdot 4\cdot e^{2x}$$=8 \cdot e^{2x}$
- $f´´´(x) = 2 \cdot 8\cdot e^{2x}$$=16 \cdot e^{2x}$
In diesem Text erklären wir dir ganz leicht, was eine e-Funktion ist, wie du eine e-Funktion ableiten kannst, wie eine Stammfunktion gebildet wird und welche Eigenschaften die e-Funktion hat. Schau dir als Grundlage am besten unsere Seite zur Kettenregel an, denn diese Ableitungsregel kannst du für dieses Thema gut gebrauchen.
E-Funktionen leicht erklärt
Die e-Funktion, auch natürliche Exponentialfunktion genannt, hat die Gleichung: $f(x) = e ^x$ (ausgesprochen: e hoch x). Die Basis ist die Eulersche Zahl. Der Exponent ist die Variable (hier $x$). Daher gehört die e-Funktion auch zu der Kategorie der Exponentialfunktionen.
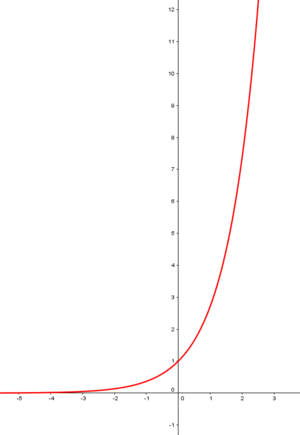
Abbildung: e-Funktion
Für diese Funktion gilt:
$e$$x$=$f(x)$=$f$ *$(x)$=...
Mann kann also die Steigung der e-Funktion an jeder Stelle $x$ mit derselben Funktion berechnen. Das ist eine Besonderheit dieser Funktion.
Merke
Eulersche Zahl
$e \approx 2,718$
Die Eulersche Zahl wurde nach dem Mathematiker Leonhard Euler benannt. Er hat im Jahr 1748 herausgefunden, dass diese Zahl der Grenzwert der unendlichen Reihe ist:
$e = 1 + \frac{1}{1} + \frac{1}{1\cdot 2} + \frac{1}{1 \cdot 2\cdot 3} + \frac{1} {1\cdot 2\cdot 3\cdot 4} + ...= \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + ...=\sum\nolimits_{n=0}^\infty \frac{1}{n!}$
$n$! wird gesprochen: n Fakultät. Es gilt zum Beispiel: 5!= 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5. Die Besonderheit ist 0!=1.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
Die e-Funktion: Eigenschaften
Monotonie
Die e-Funktion ist streng monoton wachsend und das Wachstum ist exponentiell. Das bedeutet, dass die Funktion sehr schnell ansteigt. Je größer $x$ wird, desto größer wird auch der $y$-Wert, wie wir auf der Abbildung erkennen können:
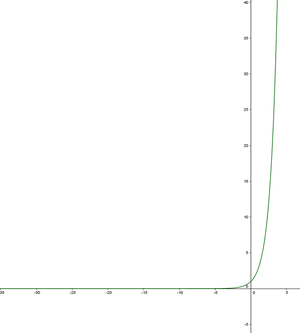
Abbildung: e-Funktion, schnelles Wachstum
Schnittpunkte mit den Achsen
Die e-Funktion hat keine Nullstellen, da eine Potenz niemals Null sein kann. Also gilt stets $f(x)$ = $e$ x ≠ $0$. Ihr Graph nähert sich mit kleiner werdendem $x$ immer mehr der $x$-Achse und es gilt $\lim\limits_{x \to -∞} $ $e$x = $0$. Diese Achse ist also eine gerade Asymptote.
Der Graph dieser Funktion schneidet die $y$-Achse an der Stelle 1, da $f(0)$ = $e$0 = $1$ ist.
Umkehrfunktion
Die Umkehrfunktion der e-Funktion ist die natürliche Logarithmusfunktion. $f(x) = e^x$ , $f^{-1} (x) = ln (x)$
Gut zu wissen
Hinweis
Umkehrfunktion von $f(x) = e^x$
$f^{-1}(x) =\log_e (x) = ln (x)$
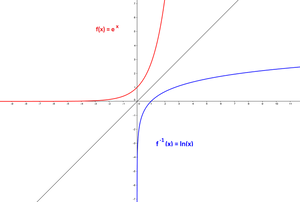
Abbildung: Funktionen $\rightarrow f^{-1}(x) = ln (x)$. Beide sind Umkehrfunktionen und damit Spiegelbilder voneinander an der Geraden $y$ = $x$.
Definitions- und Wertemenge
Für $x$ dürfen wir jede reelle Zahl einsetzen. Das bedeutet, die Definitionsmenge ist: $D_f = \mathbb{R}$
Wie wir an dem Graphen sehen, verläuft er oberhalb der x –Achse, die Asymptote ist. Der Wertebereich ist also: $ W_f = \mathbb{R^+}$. Das sind alle positiven reellen Zahlen.
Die e-Funktion ableiten und eine Stammfunktion bilden
Die Ableitung und auch die Stammfunktion der e-Funktion bildet wieder eine e-Funktion:
Merke
Ableitung: $f '(x) = e ^x $
Stammfunktion: $F (x) = e^x $
Doch wieso ist dies bei der e-Funktion der Fall?
Die allgemeine Ableitung von Exponentialfunktionen ist: $f(x) = a ^x$ $\rightarrow f ' (x) = a^x \cdot ln(a)$
Wenden wir dies auf $f(x) = e^x $ an, erhalten wir:
$ f ' (x) = (e^x)' = e^x \cdot ln(e) = e^x \cdot 1 = e^x $
Mit den Übungsaufgaben kannst du dein neu erworbenes Wissen zum Ableiten von Exponentialfunktionen prüfen. Ich wünsche dir viel Erfolg dabei!
Video: Simon Wirth
Text: Chantal Rölle
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Urheber: Simon Wirth, Fabian Serwitzki, Frank Kreuzinger, selbständiger Diplompädagoge, Pirna (Lektorat, fachliche Textkorrekturen und Grafikerstellung)
Teste dein Wissen!
Übungsaufgaben
Du möchtest mehr Aufgaben?
Teste kostenlos unser Lernportal mit vielen Übungen & Lösungen.
Du brauchst mehr Hilfe?
Wir unterstützen Dich!
Unsere Kunden über den Studienkreis
Feedback von Eltern & Schüler:innen
Klassenstufen in Mathematik
Weitere Fächer
Lernen und Üben
Noch Fragen?
Wir sind durchgehend für dich erreichbar
