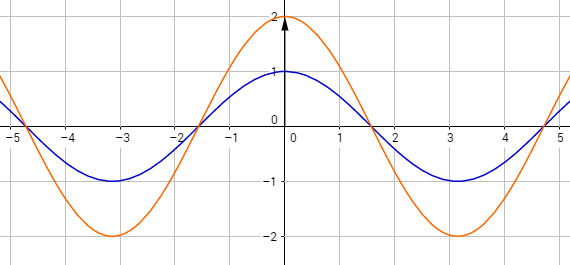
Kosinusfunktion - Streckung, Stauchung und Periode
In diesem Lerntext klären wir verschiedene Begrifflichkeiten und Bedeutungen von Variablen der allgemeinen Kosinusfunktion. Dabei gehen wir vor allem auf den Streckungsfaktor, die Periode und die Amplitude, aber auch die Ruhelage ein.
Die allgemeine Kosinusfunktion
Die Kosinusfunktion ordnet jedem Winkel eine Streckenlänge zu. Wie das passiert, kannst du auf der Seite Kosinusfunktion und ihre Eigenschaften nachlesen. Nachfolgend erklären wir dir die Bedeutung der Variablen a und b in der Funktion:
$y\;=\;\textcolor{orange}{a}\;\cdot \cos(\textcolor{green}{b}\;\cdot x)$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Streckungsfaktor $\textcolor{orange}{a}$
Die reelle Zahl $\textcolor{orange}{a}$, die in dieser Funktion als Streckungsfaktor auftritt, wirkt sich auf verschiedene Weisen auf den Verlauf der Funktion $y$=$cos(bx)$ aus. Der Streckungsfaktor $\textcolor{orange}{a}$ streckt, staucht oder spiegelt. Wie sich dieser Faktor auswirkt, zeigen wir dir in der folgenden Abbildung.
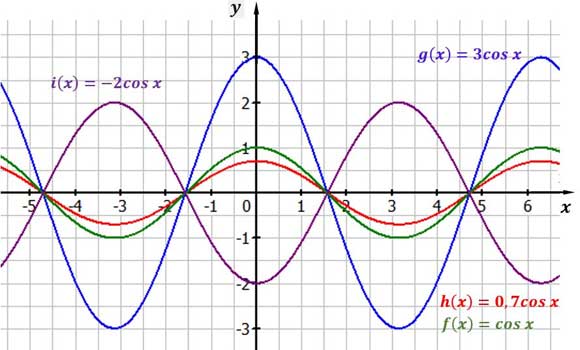
Wirkungen des Streckfaktors a auf die Funktion f(x)=cos x
Bei der blau gezeichneten Funktion $g(x)=3 cos x$ ist $a=3$. Diese Funktion ist gegenüber der grün gezeichneten Funktion gestreckt.<br/>Bei der rot gezeichneten Funktion $h(x)=0,7 cos x$ ist $a=0,7$. Diese Funktion ist gegenüber der grün gezeichneten Funktion gestaucht.<br/>Bei der lila gezeichneten Funktion $i(x)= -2 cos x$ ist $a= -2$. Diese Funktion ist gegenüber der grün gezeichneten Funktion $f(x)=cos x$ zusätzlich gespiegelt.
Merke
$\textcolor{orange}{a}$ ist zwar, wie du jetzt weißt, der Streckungsfaktor, ABER die Kosinusfunktion kann auch gestaucht werden. Du kannst dir hierbei merken:
$\textcolor{orange}a>1$ (a größer 1) $\rightarrow $ Funktion ist gestreckt.
$0<\textcolor{orange}a<1$ (a liegt zwischen 0 und 1) $\rightarrow $ Funktion ist gestaucht.
Die Veränderung des Streckungsfaktors verändert zugleich den Wertebereich der Funktion.
Merke
Die Amplitude der Kosinusfunktion wird der größte Ausschlag nach oben und unten genannt.
Die Variable $a$ der allgemeinen Kosinusfunktion bezeichnet den Streckungsfaktor. Dieser verändert die Amplitude und damit die Wertemenge.
Periode $\textcolor{green}{p}$ der Kosinusfunktion
Die Kosinusfunktion verläuft, wie die Sinusfunktion, periodisch, das heißt, dass sich die einzelnen Abschnitte der Funktion wieder und wieder wiederholen. Die Periode wird der sich immer wieder wiederholende Abschnitt genannt. Bei der Veränderung des Faktors $\textcolor{green}{b}$ verändert sich auch die Periodenlänge der Funktion. Sie verkleinert sich bei einem Faktor zwischen $-1$ und $1$ und vergrößert sich bei Werten größer $1$ und kleiner $-1$. Hierbei ist das Vorzeichen vor dem Faktor jedoch egal, es gibt keinen Unterschied zwischen negativen und positiven Faktoren.
Die kleinste Periode berechnet man mit der Formel $p = | \frac{2 \pi}{b} | $
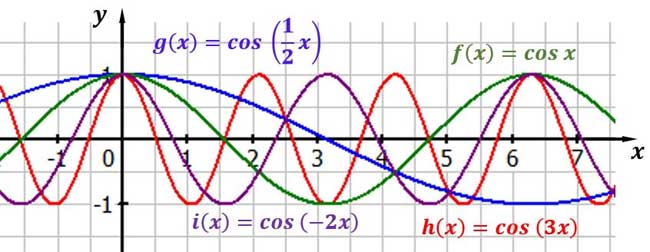
Kosinusfunktionen mit verschiedenen Periodenlaengen
Merke
Die Periode gibt die Länge eines sich wiederholenden Abschnittes an. Er kann verlängert oder verkürzt werden.
Als allgemeine Gleichung einer Kosinusfunktion wird oft $f(x)$=$a$ · $cos (bx + c) + d$ bezeichnet.
Reelle Zahlen $a, b, c$ und $d$ haben folgende Effekte:
- $a$ streckt entlang der $y$-Achse
- $b$ beeinflusst die Periode
- $c$ verschiebt entlang der $x$-Achse
- $d$ verschiebt entlang der $y$-Achse
Ruhelage der Kosinusfunktion
Ein weiterer Fachbegriff bei Kosinusfunktionen ist die Ruhelage. Diese bildet den Mittelwert zwischen Hochpunkt und Tiefpunkt. Sie wird als Gerade dargestellt. Bei keiner Verschiebung der Funktion in Richtung der y-Achse entspricht die x-Achse der Ruhelage.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Lektor: Frank Kreuzinger
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
