Was ist eine Wurzelfunktion? - Erklärungen
Die Wurzelfunktionen sind ein Spezialfall der Potenzfunktionen. Als Wurzelfunktionen bezeichnet man Potenzfunktionen deren Exponent zwischen 0 und 1 liegt. Wurzelfunktionen haben besondere Eigenschaften, die sie von den anderen Potenzfunktionen unterscheiden. Daher werden Wurzelfunktionen manchmal auch nicht explizit zu den Potenzfunktionen gezählt.
Schreibweise
Wir haben im Text über Potenzfunktionen mit rationalem Exponenten schon erfahren, dass wir eine Wurzelfunktion in eine Potenzfunktion mit einem rationalen Exponenten umschreiben können. Wenn wir eine Wurzelfunktion in eine Potenzfunktion umwandeln, entsteht eine Potenzfunktion deren Exponent ein Bruch ist. Hierzu nun ein Beispiel:
Merke
Merke
Hier klicken zum Ausklappen
Die zwei Schreibweisen für die Wurzelfunktion sind:
1. $f(x)=x^{\frac{2}{5}}$
2. $f(x)=\sqrt[5]{x^2}$
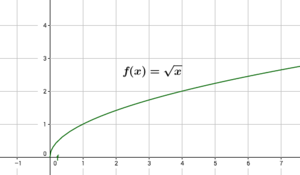
Graph der Quadratwurzelfunktion: $f(x) = \sqrt x$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Eigenschaften der Wurzelfunktion
Eine sehr wichtige Eigenschaft der Wurzelfunktion ist die Tatsache, dass unter der Quadratwurzel niemals eine negative Zahl stehen kann. Dies erklärt sich dadurch, dass die Wurzelfunktion die Umkehrfunktion der Quadratfunktion ist. Wenn wir die Wurzel aus einer Zahl ziehen, suchen wir also die Zahl, die mit sich selbst multipliziert die Zahl unter der Wurzel ergibt. Egal, ob eine Zahl positiv oder negativ ist, das Quadrat einer Zahl ist immer positiv und daher muss auch die Zahl unter der Quadratwurzel immer positiv sein.
Beispiel
Beispiel
Hier klicken zum Ausklappen
Wir gucken uns hierzu nun ein Beispiel an:
Wir haben die Gleichung: $y=\sqrt{25}$
Wie lautet die Lösung?
Die Lösung ist 5, denn $5 \cdot 5 = 25 $.
Mehr zu diesem Thema findest du in dem Lerntext zu Quadrat- und Kubikwurzeln.
Wir erkennen im Bild oben, dass es keine negativen y-Werte gibt. Das liegt daran, dass es keine reelle Zahl gibt, die mit sich selbst multipliziert eine negative Zahl ergibt. Das heißt, die Wurzelfunktion ist nur für positive x-Werte, einschließlich der Null, definiert oder mathematisch ausgedrückt: D = ℝ$_0$+.
Ein weiteres Merkmal ist die einzige Nullstelle. Diese liegt bei P(0|0). Auch gehen alle Wurzelfunktionen durch den Punkt P(1|1), unabhängig vom Grad der Wurzel.
Wenn wir uns die verschiedenen Wurzelfunktionen anschauen, fällt uns noch etwas auf. Je höher der Grad der Funktion ist, also je größer der Wurzelexponent, desto flacher verläuft der Funktionsgraph. Dies können wir gut in der Grafik erkennen. Und zuletzt fällt uns die fehlende Symmetrie auf. Die Wurzelfunktion kann nicht symmetrisch sein, da der Graph nur im ersten Quadranten des Koordinatensystems liegt.
Merke
Merke
Hier klicken zum Ausklappen
Die Wurzelfunktionen können keine negativen y-Werte annehmen. Unter der Wurzel dürfen keine negativen Zahlen auftreten. (Der Definitionsbereich ist: D = ℝ$_0$+)
Die Wurzelfunktion weist keine Symmetrie auf, da sie nur im ersten Quadranten des Koordinatensystems liegt.
Alle Wurzelfunktionen gehen durch die Punkte P1(0|0) und P2(1|1).
Die einzige Nullstelle aller Wurzelfunktionen liegt im Punkt P1(0/0).
Nun hast du eine detaillierte Übersicht darüber erhalten, was du unter einer Wurzelfunktion verstehst. Teste dein Wissen in unseren Übungen. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Lektor: Frank Kreuzinger
Teste dein Wissen!
Vereinfache die Funktion soweit wie möglich:
(Tipp: Du musst zunächst geschickt ausklammern.)
$f(x)=\sqrt{(4 \cdot x^6 + 4 \cdot x^2)}$
Kreuze die richtigen Schreibweisen der Quadratwurzelfunktion an.
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
