Quadratische Funktionen: Aufgaben mit Lösungen
Im folgenden Lerntext bearbeiten wir eine realitätsnahe Textaufgabe zum Thema quadratische Funktionen. Hierbei zeigen wir Schritt für Schritt, wie du solche Textaufgaben zu quadratischen Funktionen meistern kannst.
Quadratische Funktionen - Textaufgabe
Der Bogen einer Hängebrücke von der Form einer Parabel verläuft gemäß dem Graphen der Funktion $f(x) = -0,004x^2+1,2x-32,4$.
Die Verankerungspunkte der Brücke liegen unterhalb der durch die x-Achse markierten Straße. Im Koordinatensystem stellt eine Einheit dabei einen Meter in der Realität dar. Dabei beschreibt der x-Wert die Länge der Brücke und der y-Wert deren Höhe.
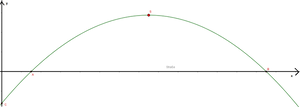
a) Wie hoch ist die Brücke (von der Straße aus gemessen)?
b) Wie lang ist die Straße auf der Brücke (Abstand $\overline{AB}$)?
c) Wie tief unterhalb der Straße befindet sich der Verankerungspunkt ($C$) der Brücke?
Im nächsten Teilkapitel erklären wir die Lösungen und gehen die einzelnen Lösungswege durch. Versuche zuerst allein die Lösung herauszufinden und schaue dann erst auf die Lösungen.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Quadratische Funktionen - Lösungen der Aufgaben
a) Wie hoch ist die Brücke (von der Straße aus gemessen)?
Die Höhe der Brücke von der Straße aus gemessen ist gesucht. Der höchste Punkt der Hängebrücke ist der Scheitelpunkt der Funktion. $\rightarrow S$ ist gesucht.
Wir haben die Gleichung der Funktion gegeben: $f(x) = -0,004x^2+1,2x-32,4$
Um den Scheitelpunkt herauszufinden, formen wir die Allgemeine Form in die Scheitelpunktform um.
Das geht so:
$f(x) = -0,004x^2+1,2x-32,4$
1. -0,004 ausklammern:
$f(x) = -0,004\cdot(x^2-300x)-32,4$
2. Quadratische Ergänzung bilden:
$f(x) = -0,004\cdot(x^2-300x+(\frac{300}{2})^2-(\frac{300}{2})^2)-32,4$
$f(x) = -0,004\cdot(x^2-300x+22500-22500)-32,4$
3. Negativen Wert ausklammern und mit der vorderen Zahl (hier -0,0004) mal rechnen:
$f(x) = -0,004\cdot(x^2-300x+22500)-0,004\cdot(-22500)-32,4$
$f(x) = -0,004\cdot(x^2-300x+22500)+90-32,4$
4. Werte verrechnen:
$f(x) = -0,004\cdot(x^2-300x+22500)+57,6$
5. Binomische Formel anwenden:
$f(x) = -0,004\cdot(x-150)^2+57,6$
Scheitelpunktform: $f(x) = -0,004\cdot(x-150)^2+57,6$
Nun muss nur noch der Scheitelpunkt, den wir bei der Aufgabe berechnet haben, abgelesen werden.
$f(x) = a\cdot(x−\textcolor{blue}d)^2+\textcolor{green}e$
Scheitelpunkt: S $(\textcolor{blue}d/\textcolor{green}e)$
Der Scheitelpunkt der Funktion liegt also bei: $S(150/57,6)$. Hier liegt auch der höchste Punkt der Brücke. Demnach beträgt die Höhe der Brücke über der Fahrbahn $57,6 m$.
Bei Schwierigkeiten beim Umformen von der Allgemeinen Form oder auch der Normalform in die Scheitelpunktform, schaue im Lerntext Normalform noch einmal nach.
b) Wie lang ist die Straße auf der Brücke (Abstand $\overline{AB}$)?
Die Länge der Straße bzw. der Abstand zwischen Punkt $A$ und $B$ ist gesucht.
Dafür müssen wir die Werte der Punkte $A$ und $B$ ermitteln. Wenn wir uns die Abbildung genauer anschauen, erkennen wir, dass $A$ und $B$ die Nullstellen der Funktion sind.
$\rightarrow$ Wir müssen bei der Aufgabe zu quadratischen Funktionen die Nullstellen ermitteln und dann den Abstand zwischen den beiden Nullstellen berechnen.
$f(x) = -0,004x^2+1,2x-32,4=0$
Nun können wir mit der p-q-Formel oder mit der Mitternachtsformel die Nullstellen bestimmen. Wir werden schrittweise die pq-Formel verwenden:
$f(x) = -0,004x^2+1,2x-32,4=0$ $|:(-0,004)$
$f(x) = x^2-300x+8100=0$
$p=-300$
$q=8100$
$x_{1/2} = -\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-{q}}$
$x_{1/2} = -\frac{-300}{2}\pm \sqrt{(\frac{-300}{2})^2-{8100}}$
$x_{1/2} = 150\pm \sqrt{22500-8100}$
$x_{1/2} = 150\pm \sqrt{22500-8100}$
$x_{1/2} = 150\pm \sqrt{14400}$
$x_{1/2} = 150\pm120$
$x_1 = 150+120=270$
$x_2 = 150-120=30$
Nun haben wir die zwei Nullstellen gefunden. Der Abstand zwischen dem Punkt $A (30/0)$ und Punkt $B (270/0)$ beträgt $240m$. ($270m-30m=240m$)
Damit ist die Straße auf der Brücke $240m$ lang.
c) Wie tief unterhalb der Straße befindet sich der Verankerungspunkt ($C$) der Brücke?
Die Tiefe des Verankerungspunkts $C$ soll herausgefunden werden. Dafür müssen wir den y-Wert des Punktes $C$ ermitteln. Wir sehen, dass der Punkt $C$ auf der y-Achse liegt, bzw. die Funktion die y-Achse im Punkt $C$ schneidet. Wir müssen also den y-Achsenabschnitt herausfinden. Da wir die Allgemeine Form gegeben haben, können wir den Wert einfach ablesen. Es ist der Wert der nicht mit $x$ oder $x^2$ mal genommen wird.
$f(x) = -0,004x^2+1,2x\textcolor{red}{-32,4}$
Die Funktion schneidet die y-Achse, wenn der x Wert gleich null ist.
$f(x) = -0,004x^2+1,2x-32,4$
$f(0) = -0,004\cdot0^2+1,2\cdot0-32,4$
$f(0) = -32,4$
Der Verankerungspunkt befindet sich $32,4m$ unterhalb der Straße.
Du hast jetzt eine Beispielaufgabe zu den quadratischen Funktionen durchgerechnet. Verbessere dein Können auch mit unseren Übungen!
Teste dein Wissen!
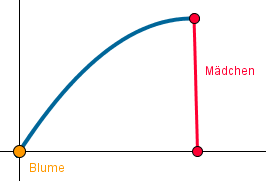
Ein Mädchen gießt eine Blume. Der Wasserstrahl hat die Form einer Parabel der Funktion $f(x) = -0,2x^2+2x $. Der Strahl trifft die Blume im Ursprung (Punkt (0/0)). Der Boden ist die x-Achse.
In welche Höhe hält das Mädchen den Wasserschlauch?
Je höher ein Feuerwerkskörper fliegen kann, umso teurer kann er verkauft werden. Daher will das Untermehmen "Fireworks" eine neue Rakete entwickeln.
Diese Rakete hat die Flugbahn $f(x) = -0,488x^2+24,4x+0,5$.
Das $y$ beschreibt die Höhe und $x$ die horizontale Entfernung.
Das Unternehmen verspricht, dass die Raktete mindestens 300m hoch fliegt.
Stimmt diese Angabe?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema





























































