Exponentialfunktionen: Erklärung und Aufgaben
Exponentialfunktionen sind besondere Funktionen. Im nachfolgenden Beispiel betrachten wir ebenfalls davon abgeleitete Funktionen.
Beispiel
$f(x) = 4^x$
$f(x) = 5^{x-2}$
$f(x) = 2 \cdot (\frac{1}{3})^x$
$f(x) = -8 \cdot 2^{x+5} + 3$
Eigenschaften
Die allgemeine Funktionsgleichung einer Exponentialfunktion lautet:
$f(x) = a^x$
Die Variable ($x$) steht im Exponenten. Die Basis (a) muss eine positive reelle Zahl sein ($a \in \mathbb{R}$, $a > 0$, $a \neq 1$). Wir unterscheiden zwei Arten von Exponentialfunktionen: Exponentialfunktionen deren Basis größer als $1$ ist und Exponentialfunktionen deren Basis zwischen $0$ und $1$ liegt.
1. Fall: $a > 1$
Exponentialfunktionen sind Funktionen der Form $f(x)$=$a$$x$, wobei $a$ eine positive reelle Zahl ungleich 1 und $x$ eine beliebige reelle Zahl ist. Je größer $a$, desto steiler verläuft der Graph. Folgend ein paar Beispiele:
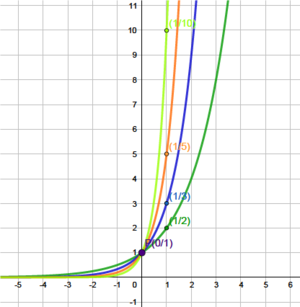
Abbildung: $\textcolor{green}{f(x)=2^x}$, $\textcolor{blue}{g(x)=3^x}$, $\textcolor{orange}{h(x)=5^x}$, $\textcolor{yellowgreen}{i(x)=10^x}$
2. Fall: $0 < a < 1$
Die Basis der Exponentialfunktion ist größer als $0$ und kleiner als $1$. Dies bedeutet, dass der Graph der Exponentialfunktion fallend verläuft. Je kleiner $a$, desto steiler verläuft der Graph. Folgend ein paar Beispiele:
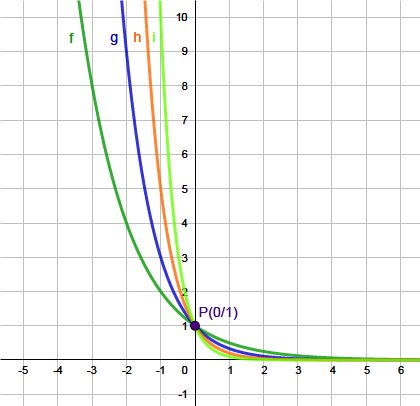
Abbildung: $\textcolor{green}{f(x)=(\frac{1}{2})^x}$, $\textcolor{blue}{g(x)=(\frac{1}{3})^x}$, $\textcolor{orange}{h(x)=(\frac{1}{5})^x}$, $\textcolor{yellowgreen}{i(x)=(\frac{1}{10})^x}$
Wenn wir uns gleichfarbige Graphen aus den beiden oberen Abbildungen ansehen, dann stellen wir fest, dass sie Bilder voneinander sind, wenn man sie an der y-Achse spiegelt.
Das liegt daran, dass ihre Basen Kehrwerte voneinander sind.
3 und 1/3 sind beispielsweise Kehrwerte voneinander.
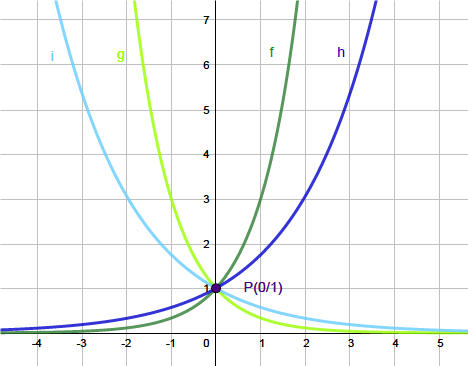
Abbildung: $\textcolor{green}{f(x)=3^x}$, $\textcolor{yellowgreen}{g(x)=(\frac{1}{3})^x}$, $\textcolor{blue}{h(x)=(\frac{7}{4})^x}$, $\textcolor{skyblue}{i(x)=(\frac{4}{7})^x}$
Methode
Der Kehrwert einer Zahl wird gebildet, indem wir Zähler und Nenner der Zahl vertauschen.
Ein paar Beispiele:
$\frac{2}{5} ~~ \rightarrow ~~$ Kehrwert: $\frac{5}{2}$
$\frac{1}{3} ~~ \rightarrow ~~$ Kehrwert: $\frac{3}{1} = 3$
$4 (=\frac{4}{1}) ~~ \rightarrow ~~$ Kehrwert: $\frac{1}{4}$
Merke
Für alle Exponentialfunktionen der Form $f(x) = a^x$ gilt:
Die x-Achse ist Asymptote für den Graphen.
Der Graph der Funktion zeigt
kein Symmetrieverhalten.
Die Funktion hat keine Nullstellen.
Der
Funktionsgraph geht durch den
Punkt $P(0\mid1)$.
Der Funktionsgraph verläuft
steigend bei $a > 1$ und fallend bei $0 < a < 1$.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Streckung parallel zur y-Achse und Spiegelung an der x-Achse
Die Funktionsgleichung einer Exponentialfunktion kann durch einen Streckfaktor b erweitert werden. Die Funktionsgleichung wird dann folgend geschrieben:
$f(x) = b \cdot a^x$
Der Streckfaktor b bewirkt, dass der Graph von a x parallel zur y-Achse gestreckt wird. Der Funktionswert wird hierbei mit dem Streckfaktor $b$ multipliziert. Wenn der Streckfaktor b negativ ist, bewirkt dies, dass der Graph von a x außerdem an der x-Achse gespiegelt wird.
Wir nehmen als Beispiel die Funktion $\textcolor{blue}{f(x) = 2^x}$.
Zunächst strecken wir diese parallel zur y-Achse mit dem Streckfaktor $\textcolor{red}{b = 3}$. Es entsteht die Funktion $\textcolor{red}{g(x) = 3 \cdot 2^x}$. Der Funktionsgraph schneidet die y-Achse bei $P(0 \mid 3)$ und verläuft insgesamt etwas $\textcolor{red}{steiler}$ als der Graph der Funktion $f(x)$.
Wir können die Funktion jedoch auch mit einem Streckfaktor, der zwischen $0$ und $1$ liegt, strecken. Wenn wir die Funktion mit dem Streckfaktor $\textcolor{green}{b = 0,5}$ strecken, entsteht die Funktion $\textcolor{green}{i(x) = 0,5 \cdot 2^x}$. Der Graph schneidet die y-Achse bei $P(0 \mid 0,5)$ und verläuft insgesamt etwas $\textcolor{green}{flacher}$ als der Graph der Funktion $f(x)$.
Wenn wir die Funktion mit einem negativen Streckfaktor strecken, wird der Graph zusätzlich zur Streckung an der x-Achse gespiegelt (siehe Graphik).
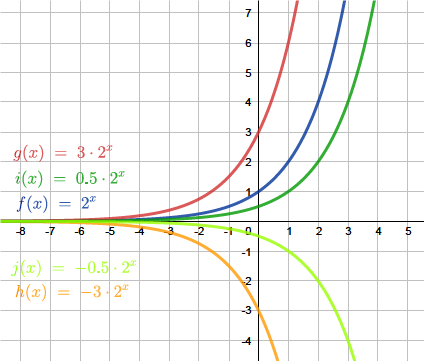
Die Funktion $f(x)=2^x$ wird parallel zur y-Achse gestreckt. Ein negativer Streckfaktor bewirkt, dass der Graph der Funktion zusätzlich an der x-Achse gespiegelt wird.
Verschiebung entlang der x-Achse
Der Graph einer Exponentialfunktion kann entlang der x-Achse verschoben werden. Die Verschiebungskonstante c bewirkt eine Verschiebung des Graphen um $c$ Einheiten parallel zur x-Achse. Wenn $c$ positiv ist, ist der Graph nach links verschoben und wenn $c$ negativ ist, ist der Graph nach rechts verschoben. Die Funktionsgleichung wird dann folgend geschrieben:
$f(x)=a^{x+c}$
Hier ein paar Beispiele:
$\textcolor{blue}{f(x)=2^x}$
$\textcolor{limegreen}{g(x)=2^{x+3}}$
$\textcolor{orange}{h(x)=2^{x-4}}$
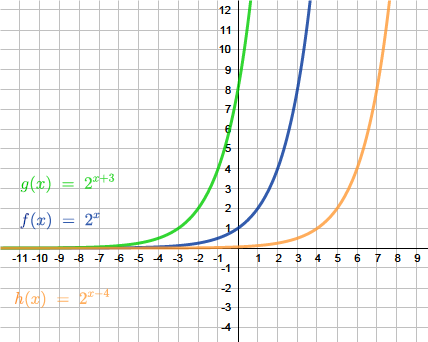
Abbildung: Verschiebung parallel zur x-Achse
Verschiebung entlang der y-Achse
Der Graph einer Exponentialfunktion kann entlang der y-Achse verschoben werden. Die Verschiebungskonstante ($d$) bewirkt eine Verschiebung des Graphen um $d$ Einheiten parallel zur y-Achse. Wenn $d$ positiv ist, ist der Graph nach oben verschoben und wenn $d$ negativ ist, ist der Graph nach unten verschoben. Die Funktionsgleichung wird dann wie folgt geschrieben:
$f(x) = a^x + d$
Hier ein paar Beispiele:
$\textcolor{blue}{f(x)=2^x}$
$\textcolor{green}{g(x)=2^x + 4}$
$\textcolor{orange}{h(x)=2^x - 3}$
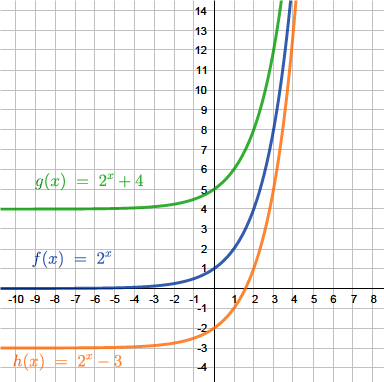
Abbildung: Verschiebung parallel zur y-Achse
Zusatz: Kombinationen
Die oben beschriebenen Streckungen und Verschiebungen können natürlich auch kombiniert werden.
Hierzu abschließend noch drei Beispiele:
$\textcolor{blue}{f(x)=2^x}$
$\textcolor{green}{g(x)=3 \cdot 2^x - 2}$
$\textcolor{orange}{h(x)=2^{x-2} + 3}$
$\textcolor{magenta}{i(x)=-2^x + 1}$
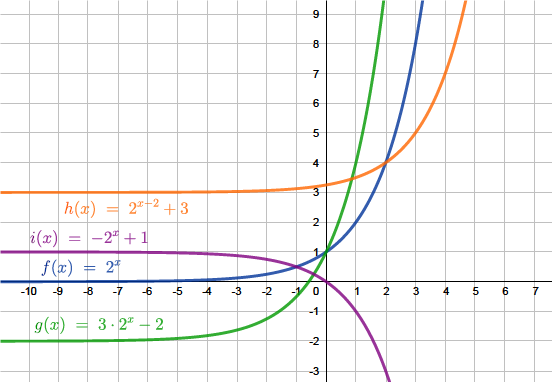
Abbildung: „schwierige" Exponentialfunktionen
Teste dein neu erlerntes Wissen nun mit unseren Übungsaufgaben. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Urheber: Simon Wirth, Fabian Serwitzki, Frank Kreuzinger
Teste dein Wissen!
Entscheide, wie der Graph der Funktion $f(x)=2^x$ verschoben wurde, um zum Graphen der Funktion $c(x)=2^{x+1}-4$ zu werden.
Kreuze die richtigen Eigenschaften der folgenden Funktion an: $h(x)= 6^x$
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
