Eigenschaften von Potenzfunktionen: Übersicht
Ihr nehmt gerade in Mathe Potenzfunktionen durch? Du willst nochmal in Ruhe alles zu diesem Thema lernen und vor allem alles verstehen? In diesem Lerntext erklären wir dir die Eigenschaften der jeweiligen Potenzfunktionen. Wir zeigen dir außerdem zu den vier Arten von Potenzfunktionen die Graphen, damit du weißt, wie sie überhaupt aussehen.
Im Folgenden findest du eine Übersicht zu den Eigenschaften von Potenzfunktionen.
Potenzfunktion - Definition
Merke
Potenzfunktionen werden laut Definition Funktionen der Form $f(x) = ax^n$ für beliebige reelle Zahlen $a$ und $n$ genannt.
Gut zu wissen
Hinweis
Wie du Potenzfunktionen zeichnest, kannst du im Lerntext Potenzfunktionen zeichnen nachlesen und lernen. Außerdem kannst du mehr über Potenzfunktionen mit natürlichen, negativen und rationalen Exponenten in unseren Lerntexten Potenzfunktionen mit natürlichem Exponenten, Potenzfunktionen mit negativem Exponenten und Potenzfunktionen mit rationalem Exponenten lernen.
Im Folgenden werden wir Potenzfunktionen mit $a=1$, also $f(x) = x^n$ behandeln. Der Exponent soll eine ganze Zahl sein.
Wir unterscheiden vier Arten von Potenzfunktionen:
1. Fall: gerader, positiver Exponent
Der Exponent der Funktion ist gerade und positiv. Der Graph einer solchen Funktion liegt oberhalb der x-Achse, also nur im ersten und zweiten Quadranten des Koordinatensystems. Die einzige Nullstelle der Funktion liegt im Ursprung. Der Graph der Funktion geht außerdem immer durch die Punkte $P_1(-1\mid1)$ und $P_2(1\mid1)$.
Merke
Potenzfunktionen mit einem positiven geraden Exponenten
Die Funktionen gehen immer durch die Punkte $P_1(-1\mid1)$, $N(0\mid0)$ und $P_2(1\mid1)$.
Die einzige Nullstelle liegt im Ursprung, $N(0\mid0)$.
Die Definitionsmenge dieser Potenzfunktionen sind alle reellen Zahlen, also $D = \mathbb{R}$.
Der Wertebereich sind alle nichtnegativen reellen Zahlen: $W: y \in \mathbb{R}, y \ge 0$.
Der Graph ist achsensymmetrisch zur y-Achse.
Für die Grenzwerte gilt: $\lim\limits_{x \to -\infty} x^n = \infty$ und $\lim\limits_{x \to \infty} x^n = \infty$
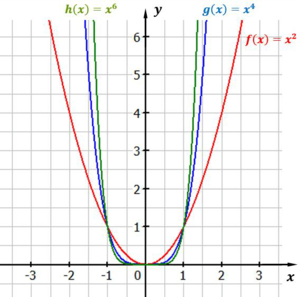
Potenzfunktionen: Exponent gerade und positiv
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
2. Fall: ungerader, positiver Exponent
Der Exponent der Funktion ist ungerade und positiv. Die Funktion verläuft, wie im Bild zu sehen, aus dem Negativen, über den Ursprung, ins Positive. Die einzige Nullstelle liegt im Punkt $N(0\mid0)$. Dieser Punkt ist Sattelpunkt für jede dieser Funktionen (außer $f(x)=x=x^1$). Alle Funktionen gehen durch die folgenden drei Punkte: $P_1(-1\mid-1)$, $N(0\mid0)$ und $P_2(1\mid1)$
Merke
Potenzfunktionen mit einem positiven ungeraden Exponenten
Die Funktionen gehen alle durch die Punkte: $P_1(-1\mid-1)$, $N(0\mid0)$ und $P_2(1\mid1)$
Die einzige Nullstelle liegt im Ursprung $(0\mid0)$.
Die Definitionsmenge und der Wertebereich sind die Menge der reellen Zahlen, also $D = \mathbb{R}$ und $W = \mathbb{R}$.
Die Funktionen sind punktsymmetrisch zum Ursprung.
Für die Grenzwerte gilt:
$\lim\limits_{x \to -\infty} x^n = -\infty$ und $\lim\limits_{x \to \infty} x^n = \infty$
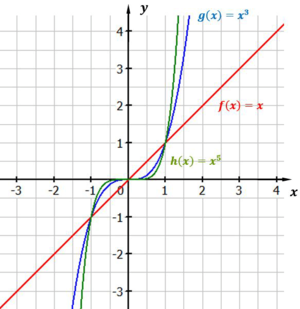
Potenzfunktionen: Exponent ungerade und positiv
3. Fall: gerader, negativer Exponent
Beim dritten Fall handelt es sich um Funktionen mit einem negativen geraden Exponenten. Der Funktionsgraph liegt auch hier nur im positiven Bereich, also oberhalb der x-Achse. Der Graph schmiegt sich an beide Koordinatenachsen an, das heißt, die Koordinatenachsen sind hier Asymptoten.
Gut zu wissen
Hinweis
Asymptoten sind in unserem Fall Geraden, an die sich unser Funktionsgraph unendlich nahe annähert. Bei der Funktion $f(x) = x^{-2}$ sind beide Koordinatenachsen Asymptoten (siehe Bild).
Merke
Potenzfunktionen mit einem negativen geraden Exponenten
Es gibt keine Nullstelle.
Die Funktionen gehen durch die Punkte $P_1(-1\mid1)$ und $P_2(1\mid1)$.
Der Definitionsbereich sind alle von Null verschiedenen reellen Zahlen: $D : x \in \mathbb{R}, x \neq 0$.
Der Wertebereich sind alle positiven reellen Zahlen $W : y \in \mathbb{R}, y > 0$.
Die Funktionen sind alle achsensymmetrisch zur y-Achse.
Für die Grenzwerte gilt:
$\lim\limits_{x \to -\infty} x^n = 0$ und $\lim\limits_{x \to \infty} x^n = 0$. Die x-Achse ist also Asymptote.
Ferner gilt:
$\lim\limits_{\substack{x \to 0 \\ x < 0}} x^n = \infty$ und $\lim\limits_{\substack{x \to 0 \\ x > 0}} x^n = \infty$. Die y-Achse ist also Asymptote
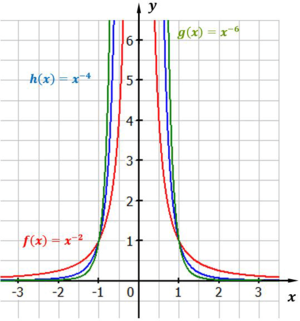
Potenzfunktionen gerade und negativ
4.Fall: ungerader, negativer Exponent
Der letzte Fall behandelt Funktionen, die einen ungeraden negativen Exponenten besitzen. Solche Funktionen sind ebenfalls, wie Funktionen mit ungeradem positivem Exponenten, punktsymmetrisch zum Ursprung.
Merke
Potenzfunktionen mit einem negativen ungeraden Exponenten
Die Funktionen gehen durch die Punkte $P_1(-1\mid-1)$ und $P_2(1\mid1)$.
Es gibt keine Nullstelle.
Der Definitionsbereich sind alle von Null verschiedenen reellen Zahlen: $D : x \in \mathbb{R}, x \neq 0$. Der Wertebereich sind alle von Null verschiedenen reellen Zahlen: $W : y \in \mathbb{R}, y \neq 0$.
Die Funktionen sind punktsymmetrisch zum Ursprung.
Für die Grenzwerte gilt:
$\lim\limits_{x \to -\infty} x^n = 0$ und $\lim\limits_{x \to \infty} x^n = 0$. Die x-Achse ist also Asymptote.
Ferner gilt:
$\lim\limits_{\substack{x \to 0 \\ x < 0}} x^n = -\infty$ und $\lim\limits_{\substack{x \to 0 \\ x > 0}} x^n = \infty$. Die y-Achse ist also Asymptote
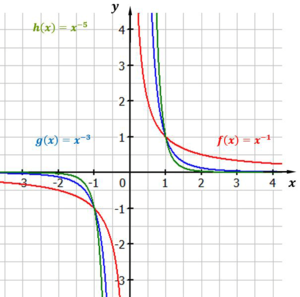
Potenzfunktionen ungerade und negativ
Potenzfunktionen - Sonderfall
Ein Sonderfall bei den Potenzfunktionen ist die Funktion, deren Exponent 0 ist, $f(x) = x^0$. Der Graph dieser Funktion ist eine Parallele zur y-Achse, die durch den Punkt P(0|1) verläuft.
Sonderfall: Potenzfunktionen mit dem Exponenten Null
Nun hast du eine detaillierte Übersicht über die unterschiedlichen Potenzfunktionen in Mathe. Ob du alles verstanden hast, kannst du anhand unserer Übungen testen. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Urheber: Simon Wirth, Fabian Serwitzki, Frank Kreuzinger
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
