Potenzfunktionen mit rationalem Exponenten
Wie bei den Themen Potenzfunktionen mit natürlichem Exponenten und Potenzfunktionen mit negativem ganzem Exponenten gibt es auch beim Thema Potenzfunktionen mit rationalem Exponenten einiges zu beachten. Alle Eigenschaften und auch ein paar Übungen zu dieser Art der Potenzfunktionen findest du auf dieser Seite.
Schreibweise der Funktion
Wir haben gelernt mit Potenzfunktionen mit geradem, ungeradem und auch negativem ganzem Exponenten zu rechnen. Doch treffen wir auch manchmal auf Potenzfunktionen, die keinen ganzzahligen Exponenten besitzen. Also zum Beispiel auf diese Funktion:
$ f(x) = x^{ \frac{1}{2}}$
Wie rechnen wir mit dieser Funktion? Wenn wir einen Wert einsetzen, etwa 4, dann erhalten wir als Ergebnis 2, wenn wir 9 einsetzen, erhalten wir als Ergebnis 3. Diese Werte stimmen mit denen der Wurzelfunktion überein. Das liegt daran, dass dies die zweite Schreibweise für die Wurzelfunktion ist. Somit wäre unsere Funktion umgeschrieben:
$f(x) = \sqrt{x}$
Der Wert zwei im Bruch entspricht also dem zweiten Grad der Wurzel, den wir bei der $_"$normalen" Wurzel weglassen, weil wir sie so oft verwenden. Jedoch erinnern wir uns an die Bedeutung davon: Wir wollen eine positive Zahl finden, die mit sich selbst multipliziert die Zahl unter der Wurzel ergibt. Das ist die Bedeutung der zweiten Wurzel. Wenn wir also eine Wurzel mit dem Wurzelgrad 3 haben, so suchen wir eine positive Zahl, die drei Mal mit sich selbst multipliziert die Zahl unter der Wurzel ergibt. Ein Beispiel hierfür ist die Funktion:
$f(x) =27^{\frac{1}{3}}~~\leftrightarrow ~~f(x) = \sqrt[3]{27}$
Hier ist die Lösung 3, denn: $3 \cdot 3\cdot 3= 27$
Merke
Potenzfunktionen mit rationalem Exponenten haben zwei Schreibweisen:
1. $f(x) = x^{\frac{n}{m}}$
2. $f(x) = \sqrt[m]{x^n}$
Natürlich kann es auch vorkommen, dass der Bruch im Exponenten negativ ist, also einen Wert wie $-\frac {1}{3}$ oder $-\frac{3}{7}$ annimmt. Solch eine Potenz wird dann ein wenig anders als Wurzel umgeschrieben. Es entsteht auch bei der Wurzelschreibweise ein Bruch. Ein Beispiel:
$f(x) = x^{-\frac{3}{7}}$ $\leftrightarrow$ $f(x)= \frac{1}{\sqrt[7]{x^3}}$
Wenn der Exponent einer Potenzfunktion ein Bruch ist, egal ob positiv oder negativ, darf man den Bruch selbstverständlich kürzen, wenn möglich.
Merke
Brüche in Potenzfunktionen darf man kürzen:
$f(x) = x^{\frac{3}{9}} ~~\rightarrow~~f(x) = x^{\frac{1}{3}}$
Potenzfunktionen werden mitunter so geschrieben:
$f(x) = x^{-\frac{n}{m}}$ $\leftrightarrow$ $f(x)= \frac{1}{\sqrt[m]{x^n}}$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Eigenschaften der Funktion
Potenzfunktionen mit rationalen Exponenten sehen oft sehr kompliziert aus. Im Folgenden nun ein paar Beispiele:
Beispiel
Betrachten wir die Funktion $f(x) = x^\frac{7}{3}$. Die Funktion ist eine Funktion mit einem rationalen Exponenten. Der Graph der Funktion sieht wie folgt aus:
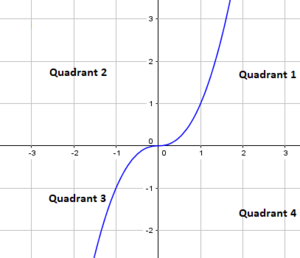
Potenzfunktion: $f(x)=x^{\frac{7}{3}}$
Diese Funktion ähnelt im ersten Quadranten den Funktionen mit ungeradem ganzem Exponenten. Das kommt dadurch, dass eine ungerade Zahl im Zähler des Exponenten steht. Bei Potenzfunktionen mit ungeradem ganzem Exponenten gibt es einen Teilgraphen im III. Quadranten, der Spiegelbild des Graphen im I. Quadranten am Ursprung ist. Dieser Teil ist nicht vorhanden, da eine Wurzel für negative Zahlen nicht definiert ist.
Analog verhält es sich mit Potenzfunktionen, deren Exponent ein Bruch mit einer geraden Zahl im Zähler ist. Diese haben die Eigenschaften von Potenzfunktionen mit geraden natürlichen Exponenten, wie uns das folgende Bild verdeutlicht:
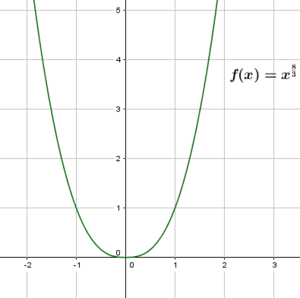
Potenzfunktion: $f(x)=x^\frac{8}{3}$
Wir können auch mit Potenzfunktionen, deren Exponenten rationale Zahlen sind, rechnen. Es gelten dieselben Regeln wie bei allen anderen Potenzfunktionen. Der einzige Unterschied ist das komplizierte Aussehen. Betrachten wir als Beispiel folgende Aufgabe:
$ \sqrt[3]{3} \cdot \sqrt[5]{3^2}$
Um die Potenzgesetze anwenden zu können, müssen die Wurzeln zunächst in Potenzen umgeformt werden.
$ 3^ \frac{1}{3} \cdot 3^ \frac{2}{5}= 3^ {\frac{1}{3}+\frac{2}{5}} = 3^ {\frac{5}{15}+\frac{6}{15}} = 3^ \frac{11}{15}$
$3^ \frac{11}{15} = \sqrt[15]{3^{11}}$
Um die Exponenten addieren zu können, haben wir die Brüche gleichnamig gemacht (auf einen gemeinsamen Nenner erweitert).
Merke
Wir stellen fest: Potenzgesetze gelten auch für Potenzen mit rationalem Exponenten.
Beispiel
a) $ 6^{-\frac{1}{2}} \cdot 6^ \frac{2}{3} = 6^{-\frac{1}{2}+ \frac{2}{3}} = 6^{- \frac{3}{6}+ \frac{4}{6}} =6^{\frac{1}{6}}$
$6^{\frac{1}{6}} = \sqrt[6]{6}$
b) $(6^{\frac{2}{5}})^\frac{5}{4} = 6^{\frac{2}{5}\cdot\frac{5}{4}}$
gekürzt ergibt sich: $6^\frac{1}{2} = \sqrt[2]{6}$
Ein Spezialfall der Potenzfunktionen mit rationalem Exponenten sind die Funktionen mit einer Zahl zwischen 0 und 1 im Exponenten. Diese werden auch Wurzelfunktionen genannt. Hier dazu mehr!
Jetzt hast du einen detaillierten Überblick über die Potenzfunktionen mit rationalem Exponenten erhalten. Ob du alles verstanden hast, kannst du anhand unserer Übungen testen. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Urheber: Simon Wirth, Fabian Serwitzki, Frank Kreuzinger, selbständiger Diplompädagoge, Pirna (Lektorat, fachliche Textkorrekturen und Grafikerstellung)
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
