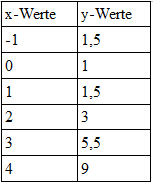Quadratische Funktionen zeichnen
Quadratische Funktionen begegnen dir öfter als du glaubst. Wir schauen uns hier zunächst einmal an, was eine quadratische Funktion ist, um sie dann zeichnen zu können.
Was ist eine quadratische Funktion?
Bei quadratischen Funktionen handelt es sich um ganzrationale Funktionen der Form $f(x) = ax^2 + bx + c$, wobei $a$, $b$ und $c$ reelle Zahlen mit $a \neq 0$ sind. Das bedeutet auch, dass es für jeden y-Wert (abgesehen von dem des Scheitelpunkts) zwei x-Werte gibt!
Schauen wir uns als Beispiel die quadratische Funktion $f(x) = 0,5x^2 - 4x + 6$ an:
Dies ist der Graph der Funktion $f(x) = 0,5x^2 - 4x + 6$
Zu dem y-Wert $2,5$ gibt es zwei x-Werte, nämlich $1$ und $7$. Wie zu erkennen ist, gilt dies für alle y-Werte außer für den des Scheitelpunkts.
Auch im Alltag begegnen dir quadratische Funktionen. Bei vielen Brücken ist eine Parabel zu sehen.
Parabel ist eigentlich nur ein anderes Wort für die typische Form einer quadratischen Funktion, welche du noch näher kennenlernen wirst.
Anlegen einer Wertetabelle
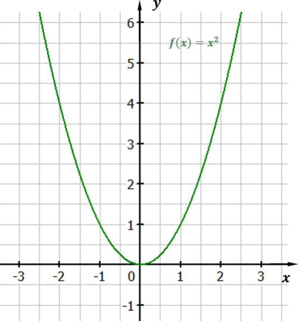
Erst einmal schauen wir uns den Graphen der Funktion $f(x) = x^2$ an. Dazu können wir eine Wertetabelle erstellen. Wir setzen für $x$ beliebige Werte ein und erhalten durch Ausrechnen den zugehörigen y-Wert.
| x-Werte | y-Werte |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Wertetabelle für $f(x) = y = x^2$
Punkte ins Koordinatensystem eintragen
Nun haben wir schon 9 Punkte, die wir in unser Koordinatensystem eintragen können. Für die negativen x-Werte, also $-1$, $-2$, $-3$ und $-4$, ergeben sich hier dieselben y-Werte wie für $1$, $2$, $3$ und $4$, denn $-1\cdot(-1) = 1$, $-2\cdot(-2) = 4$ und so weiter. Das ist in unserem Beispiel, nicht aber bei jeder quadratischen Funktion so.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Graph zeichnen
Versuche nun einmal den Graphen selber zu zeichnen, indem du die Punkte miteinander verbindest. Schaue dir dann die Abbildung an und vergleiche sie mit deiner Zeichnung.
Abbildung der Funktion
Dies ist der Graph der Funktion $f(x) = x^2$. Das ist die Normalparabel.
Beispielaufgabe: Zeichnen einer quadratischen Funktion
Ein anderes Beispiel mit einer kleinen Veränderung ist die Funktion $f(x) = x^2+1$. Zuerst erstellen wir wieder unsere Wertetabelle.
| x-Werte | y-Werte |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 5 |
| 3 | 10 |
| 4 | 17 |
Wertetabelle für $f(x) = y = x^2 + 1$
Aus der Tabelle können wir wieder Punkte entnehmen und die in unser Koordinatensystem einzeichnen. Und genau wie eben kann für den negativen x-Wert der gleiche Wert von y eingezeichnet werden. Daher ist es beim Einzeichnen hilfreich, zuerst den positiven und dann direkt den negativen Wert einzuzeichnen. Somit musst du nicht zweimal nach dem y-Wert suchen.
Zeichne nun die Funktion selber oder überlege was mit deiner Funktion $f(x) = x^2$ passiert.
Abbildung der verschobenen Funktion
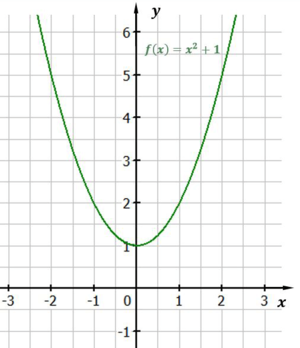
Wie du siehst, wurde unsere Funktion von eben ($f(x) = x^2$) um 1 Einheit nach oben verschoben.
In der Gleichung wird eine Verschiebung der Normalparabel durch das Addieren einer positiven oder negativen Zahl bewirkt. Die Verschiebung nach oben wird bewirkt, indem zu $x^2$ eine positive Zahl addiert wird. So gibt es zum Beispiel auch die Funktion $g(x) = x^2+99$ bei der die Normalparabel um 99 Einheiten nach oben verschoben wird.
Die Verschiebung nach unten wird bewirkt, indem eine negative Zahl zu $x^2$ hinzugerechnet wird. Ein einfaches Beispiel ist $f(x) = x^2-1$. Hier wird der Graph um 1 Einheit nach unten verschoben und sieht dann so aus:
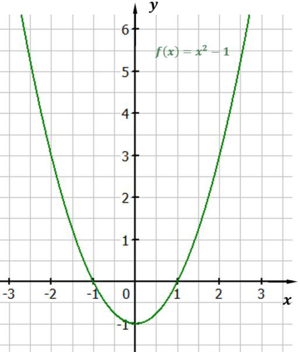
Dabei sieht man jetzt die Nullstellen. Das sind die Stellen, wo die Parabel die x-Achse schneidet. Bei dem oberen Graph sind $A(-1\mid0)$ und $B(1\mid0)$ die Punkte, in denen der Graph die x-Achse schneidet. Die Nullstellen sind demnach $x_{1} = -1$ und $x_{2} = 1$.
So jetzt weißt du, was eine quadratische Funktion ist und wie du sie zeichnen kannst. Ein wesentlicher Unterschied zur linearen Funktion ist, dass du für jeden y-Wert (außer dem des Scheitelpunkts) zwei x-Werte erhältst.
Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben. Wir wünschen dabei viel Spaß!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Lektor: Frank Kreuzinger
Teste dein Wissen!
Zeichne die Funktion: $f(x) = 2\cdot(x+5)^2-3$
Wenn du dir nicht sicher bist, wie du die Funktion zeichnen sollst, lese dir den Text zur Scheitelform durch.
Welche Funktion ist die Richtige?
Zeichne die Funktion $f(x) = x^2-5$.
Erstelle dafür zuerst eine Wertetabelle und zeichne die Punkte dann in ein passendes Koordinatensystem ein.
Welches ist die richtige Funktion?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
