In diesem Lerntext beschäftigen wir uns mit der Frage, wie man die Schnittpunkte von Funktionen mit den Achsen des Koordinatensystems berechnet.
Funktionsgraphen werden in ein Koordinatensystem eingezeichnet. Dabei kann der Funktionsgraph die Koordinatenachse schneiden oder auch nur berühren. Diese Stellen werden auch Achsenabschnitte genannt.
In diesem Lerntext erklären wir dir, wie die Schnittpunkte mit den Achsen berechnet werden.
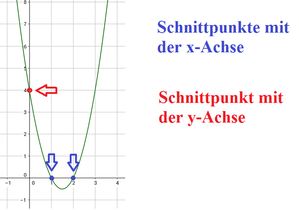
Abbildung: Schnittpunkte mit den Koordinatenachsen
Die Abbildung zeigt eine Funktion, die zwei Schnittpunkte mit der x-Achse und einen Schnittpunkt mit der y-Achse hat. Die nachfolgende Abbildung zeigt, wie die Achsen bezeichnet werden:
Gut zu wissen
Hinweis
Abbildung: Koordinatensystem
Wir sehen, dass die x-Achse von links nach rechts verläuft und die y-Achse von unten nach oben.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
Schnittpunkte mit der x-Achse
Die Schnittstellen mit der x-Achse werden auch Nullstellen genannt. Um diese zu ermitteln, muss die Funktion gleich null gesetzt werden. Anders gesagt muss der y-Wert den Wert null haben. Wenn wir uns das Koordinatensystem anschauen, ist dies logisch, da die x-Achse auf der Höhe von $y=0$ verläuft.
Methode
$f(x) = 0 \rightarrow$ Schnittpunkt(e) mit der x-Achse
Es gibt je nach Art der Funktion verschiedene Möglichkeiten die Nullstellen zu berechnen. Dazu gehört bei quadratischen Funktionen zum Beispiel die p-q-Formel oder bei Funktionen mit $x^3$ die Polynomdivision.
Schnittpunkt mit der y-Achse
Die Schnittstelle mit der y-Achse wird auch y-Achsenabschnitt genannt. Wichtig dabei ist, dass es nur einen einzigen Schnittpunkt geben kann. Dies liegt daran, dass jedem x-Wert einer Funktion nur maximal ein y-Wert zuordnet werden kann. Der x-Wert, an dem die Funktion die y-Achse schneidet, ist immer null.
Methode
$x=0 \rightarrow$ Schnittpunkt mit der y-Achse
Beispielaufgabe: Schnittpunkte mit den Koordinatenachsen bestimmen
Beispiel
Was sind die Schnittpunkte der Funktion $f(x) = 2x^2+3x-1$ mit den Koordinatenachsen?
x-Achse
$f(x) = 0$
$f(x) = 2x^2+x-3 = 0$
Wir lösen die Gleichung mit der Mitternachtsformel
$x_1 =-1,5 $
$x_2 = 1$
$P_1(-1,5/0)$
$P_2(1/0)$
$~$
y-Achse
$x=0$
$f(0) = 2\cdot 0^2+0-3 = -3$
$f(0)=y =-3$
$P_3(0/-3)$
Die Funktion schneidet die x-Achse an den Punkten $P_1(-1,5/0)$, $P_2(1/0)$ und die y-Achse am Punkt $P_3(0/-3)$.
Mit den Übungsaufgaben kannst du dein Wissen überprüfen. Viel Erfolg dabei!
Video: Simon Wirth
Text: Chantal Rölle
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Urheber: Simon Wirth, Fabian Serwitzki, Frank Kreuzinger, selbständiger Diplompädagoge, Pirna (Lektorat, fachliche Textkorrekturen und Grafikerstellung)
Teste dein Wissen!
Übungsaufgaben
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Du möchtest mehr Aufgaben?
Teste kostenlos unser Lernportal mit vielen Übungen & Lösungen.
Du brauchst mehr Hilfe?
Wir unterstützen Dich!
Unsere Kunden über den Studienkreis
Feedback von Eltern & Schüler:innen
Weitere Erklärungen & Übungen zum Thema
Mathematik
> Funktionen
Klassenstufen in Mathematik
Weitere Fächer
Lernen und Üben
Noch Fragen?
Wir sind durchgehend für dich erreichbar
