Potenzfunktionen zeichnen
Potenzfunktionen sind ein wichtiges Thema der Mathematik. Sie sind zu Anfang noch einfach und werden mit der Zeit immer komplexer. Dennoch wird erwartet, dass du auch komplexe Potenzfunktionen zeichnen bzw. mindestens skizzieren kannst. Doch wie soll man die Funktion $f(x)=5 \cdot (x-1)^8 +7 $ zeichnen?
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Potenzfunktionen zeichnen - Vorgehensweise
Um die Funktion zu zeichnen brauchen wir Kenntnisse von den verschiedenen Potenzfunktionen und ihren jeweiligen Graphen. Mit diesem Wissen im Hinterkopf gucken wir uns einfach den größten Exponenten der Funktion an und können dann entscheiden, wie der Grundverlauf des Funktionsgraphen aussieht.
Der größte Exponent ist hier 8. Die Grundform ist eine Potenzfunktion vom Grad 8. Das Bild ist daher eine Parabel, da die Grundform eine Potenzfunktion mit geradem positivem Exponenten ist.
Der nächste Schritt ist das Herausfinden des Streckfaktors der Funktion. Ob dieser positiv oder negativ ist, hat einen großen Einfluss auf den Verlauf der Parabel. Unsere Funktion besitzt den Streckfaktor $5$. Die Parabel ist also nach oben geöffnet und stark gestreckt.
Merke
Merke
Hier klicken zum Ausklappen
Der Streckfaktor bestimmt den Verlauf der Funktion. Der Streckfaktor bestimmt, ob der Graph nach oben oder nach unten geöffnet ist und ob der Graph gestreckt oder gestaucht ist.
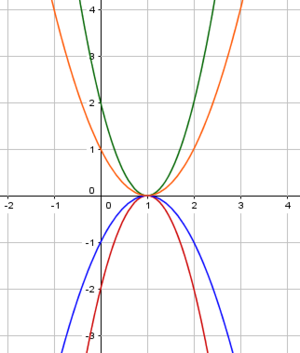
Potenzfunktionen mit unterschiedlichen Streckfaktoren
Nachdem nun Art und Verlauf der Funktion bestimmt wurden, wird nun die Verschiebung entlang der Koordinatenachsen ermittelt. Diese ist in unserer Funktion $f(x)=5 \cdot (x \textcolor{green}{-1})^8 \textcolor{blue}{+7} $ durch die markierten Zahlen gegeben. Diese zeigen uns, dass der Funktionsgraph um $1$ nach rechts und um $7$ nach oben verschoben wird, ausgehend vom Ursprung.
Fassen wir alle Informationen zusammen, erhalten wir:
Die Funktion $f(x)= \textcolor{red}{5} \cdot (x \textcolor{green}{-1})^\textcolor{orange}{8} \textcolor{blue}{+7} $ ist
$\textcolor{red}{nach\; oben\; geöffnet}$
$\textcolor{red}{um\; 5\; gestreckt}$
$\textcolor{orange}{bildet \; eine \; Parabel}$
$\textcolor{green}{um \;1 \;nach \;rechts \;verschoben}$
$\textcolor{blue}{um\; 7\; nach \;oben\; verschoben}$
Wir setzen also bei P1(1|7) unseren ersten Punkt, da wir wissen, dass der Graph eine verschobene Parabel ist, die dort ihren Scheitelpunkt hat. Der nächste Punkt wäre bei einer Streckung von $1$ bei P2(2|8). Da der Streckfaktor aber $5$ ist, muss der y-Wert um $5$ nach oben verschoben werden und somit liegt der zweite Punkt bei P2(2|12).
Aus der Achsensymmetrie der Funktion x8 folgt, dass der dritte Punkt bei P3(0|12) liegt. Nun haben wir drei Punkte, mit deren Hilfe wir den Graphen skizzieren können, siehe Abbildung oben. Der Graph der Funktion ist recht steil, was an dem relativ großen Exponenten $8$ liegt. Es gilt: Je größer der Exponent der Funktion, desto steiler ist der Funktionsgraph.
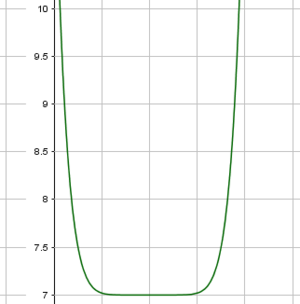
Wertetabelle erstellen
Wenn man den Graphen möglichst genau zeichnen möchte, sollte man eine Wertetabelle erstellen. Diese ermöglicht sehr genaues Zeichnen, da mehrere Punkte des Graphen ermittelt werden. Du beginnst mit dem Scheitelpunkt der Funktion, hier also mit dem Punkt P(1|7) und berechnest dann die y-Werte der benachbarten Punkte. Das heißt, du berechnest zunächst die Funktionswerte für $x=0$ und $x=2$, dann die Funktionswerte für $x=-1$ und $x=3$.... Im Heft sieht das dann etwa so aus:
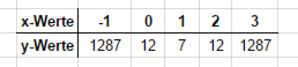
Wertetabelle zur Beispielfunktion
Die Funktionswerte können sehr schnell sehr groß werden. Das hängt vor allem von der Größe des Exponenten ab. Je größer der Exponent, desto schneller $_"$wächst$"$ die Funktion. Es ist also ratsam zu überlegen, wie groß die Schritte für die Tabellen gewählt werden sollten.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Lektor: Frank Kreuzinger
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
