Monotonie von Potenzfunktionen bestimmen
In diesem Lerntext beschäftigen wir uns mit den verschiedenen Arten der Monotonie von Potenzfunktionen.
Es gibt verschiedene Arten von Potenzfunktionen, deren Monotonieverhalten sich unterscheidet. Daher schauen wir uns in diesem Text die Monotonie von Potenzfunktionen genau an.
Merke
Potenzfunktionen sind Funktionen der Form $f(x) = a \cdot x^{n}$, wobei $a$ und $n$ beliebige reelle Zahlen sind.
Hierbei werden die Funktionen, abhängig vom Exponenten, in vier verschiedene Fälle unterteilt:
- gerader, positiver Exponent
- gerader negativer Exponent
- ungerader, positiver Exponent
- ungerader negativer Exponent
Was Monotonie bedeutet und wie sie von jeder beliebigen Funktion bestimmt werden kann, erfährst du hier: Monotonie
Schauen wir uns zunächst das Monotonieverhalten für eine Potenzfunktion mit geradem, positivem Exponenten an:
Monotonie von Potenzfunktionen mit geradem, positivem Exponenten
Beispiel
Ein Beispiel für diese Art von Potenzfunktionen ist: $f(x) = x^2$
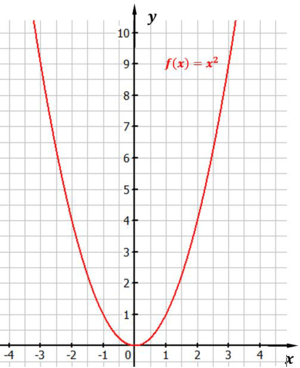
Abbildung: Funktion $f(x) = x^2$
Wir sehen, dass die Funktion im Punkt $P(0/0)$ einen Tiefpunkt hat. Jede Potenzfunktion mit geradem, positivem Exponenten besitzt im gleichen Punkt einen Tiefpunkt. Für $ x \le 0$ ist die Funktion streng monoton fallend, für $x \ge 0$ ist die Funktion streng monoton wachsend (steigend).
Merke
Für die Normalparabel kann in ihrer Gesamtheit kein Monotonieverhalten angegeben werden.
Betrachtet man einzelne Intervalle, so stellt man fest:
Für $x \le 0$ ist die Funktion monoton fallend.
Für $x \ge 0$ ist die Funktion monoton wachsend (steigend).
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Monotonie von Potenzfunktion mit geradem, negativem Exponenten
Beispiel
Ein Beispiel für eine Potenzfunktion mit geradem, negativem Exponenten ist: $f(x) = x^{-4}$
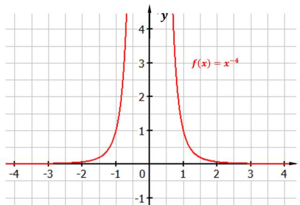
Abbildung: Funktion $f(x) = x^{-4}$
Die Funktion hat keinen Hoch- oder Tiefpunkt. Je näher der x-Wert an Null kommt, desto größer wird der y-Wert. In der Abbildung können wir sehen, dass die Funktion für alle x-Werte kleiner Null, streng monoton steigend ist und für alle Werte größer Null streng monoton fallend ist.
Merke
Diese Funktion ist in ihrer Gesamtheit weder monoton fallend noch monoton steigend.
Beschränkt man sich jedoch auf die Intervalle, gilt Folgendes:
Für $x < 0$ verläuft die Funktion streng monoton wachsend (steigend).
Für $x > 0$ verläuft die Funktion streng monoton fallend.
Für $x = 0$ ist die Funktion nicht definiert.
Monotonie von Potenzfunktionen mit ungeradem, positivem Exponenten
Beispiel
Ein Beispiel für eine Potenzfunktion mit ungeradem, positivem Exponenten ist: $f(x) = x^{3}$
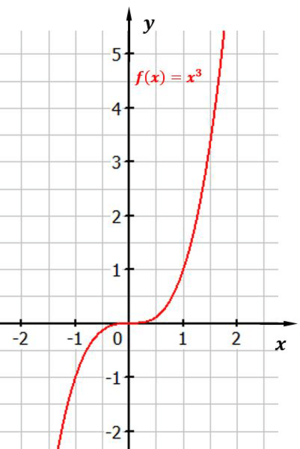
Abbildung: Funktion $f(x) = x^{3}$
Funktionen mit ungeradem, positivem Exponenten haben am Punkt $P(0/0)$ einen Sattelpunkt. An dieser Stelle ist die Steigung gleich Null.
Wir sehen, dass die Funktion für jedes $x$ steigt.
Merke
Für diese Funktion gilt also für alle $x$:
Die Funktionswerte (y-Werte) nehmen mit zunehmenden x-Werten zu – die Funktion ist also streng monoton steigend.
Monotonie von Potenzfunktionen mit ungeradem, negativem Exponenten
Beispiel
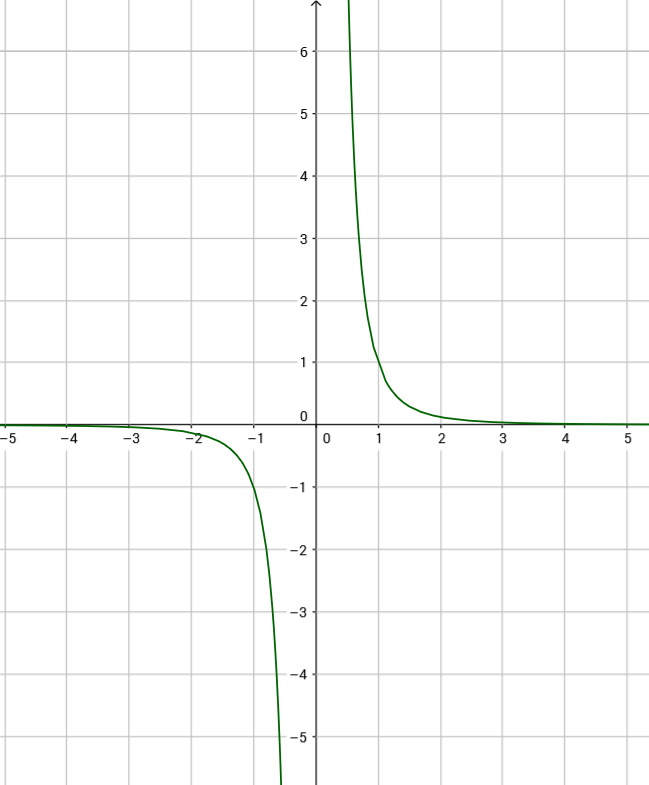
Ein Beispiel für eine Potenzfunktion mit ungeradem, negativem Exponenten ist: $f(x) = x^{-3}$
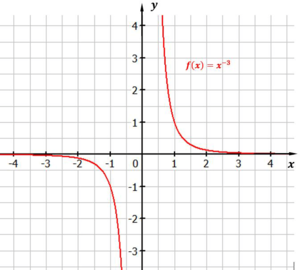
Abbildung: Funktion $f(x) = x^{-3}$
Je weiter sich der x-Wert von links der Null nähert, desto kleiner wird der zugehörige Funktionswert. Die y-Werte gehen gegen minus Unendlich. Der Funktionsgraph nähert sich der y-Achse immer mehr, ohne sie zu erreichen. Die y-Achse ist Asymptote.
Je größer der x-Wert wird, desto mehr nähern sich die y-Werte der x-Achse. Diese Werte gehen gegen Null, ohne die x-Achse zu erreichen. Die x-Achse ist ebenfalls Asymptote.
Die Funktion ist also stets streng monoton fallend.
Merke
Diese Funktion ist in ihrer Gesamtheit monoton fallend.
Betrachtung der Intervalle:
Für $x < 0$ verläuft die Funktion streng monoton fallend.
Für $x > 0$ verläuft die Funktion streng monoton fallend.
Für $x = 0$ ist die Funktion nicht definiert.
Nun weißt du, was das Monotonieverhalten von Potenzfunktionen ist. Mit den Übungsaufgaben kannst du dein Wissen testen. Viel Erfolg dabei!
Video: Simon Wirth
Text: Chantal Rölle
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Urheber: Simon Wirth, Fabian Serwitzki, Frank Kreuzinger, selbständiger Diplompädagoge, Pirna (Lektorat, fachliche Textkorrekturen und Grafikerstellung)
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
