Kurvendiskussion - Beispielaufgabe mit Lösung
In diesem Text schauen wir uns ein Beispiel einer typischen Kurvendiskussion an. Wir gehen mit dir Schritt für Schritt die zu bearbeitenden Punkte durch.
Gerne kannst du dir vorher nochmal eine Übersicht über die Kurvendiskussion verschaffen.
Kurvendiskussion - Beispielaufgabe mit Lösung
In unserem Beispiel zur Kurvendiskussion wird die Funktion $f(x) = x^2-3x+2$ behandelt.
1. Definitionsmenge
Die Definitionsmenge der obigen Aufgabe zur Kurvendiskussion besteht aus allen Zahlen, die für die Variable $x$ eingesetzt werden dürfen.
$f(x) = x^2-3x+2$
Welche Werte dürfen für $x$ eingesetzt werden? Es darf jede beliebige Zahl eingesetzt werden. $\rightarrow D_f= \mathbb{R} $
Der Definitionsbereich besteht aus reellen Zahlen.
2. Schnittpunkte mit den Koordinatenachsen
1. Nullstellen
Um die Nullstellen der Funktion zu berechnen, müssen wir den Funktionsterm gleich null setzen.
$f(x) = 0$
$f(x)=x^{2}-3x+2=0$
Anschließend verwenden wir die p-q-Formel, um die Nullstellen zu berechnen:
$p=-3$ und $q=2$
$x_{1/2} = \frac{- p}{2}\pm \sqrt{(\frac{p}{2})^2- q}$
$= -\frac{- 3}{2}\pm \sqrt{(\frac{- 3}{2})^2- 2}$
$= +\frac{ 3}{2}\pm \sqrt{\frac{9}{4}- \frac{2}{1}}$
$= \frac{ 3}{2}\pm \sqrt{\frac{9}{4}- \frac{8}{4}}$
$= \frac{ 3}{2}\pm \sqrt{\frac{1}{4}}$
$= \frac{ 3}{2}\pm \frac{1}{2}$
$x_{1} = \frac{ 3}{2} + \frac{1}{2} = \frac{4}{2} = 2$
$x_{2} = \frac{ 3}{2} - \frac{1}{2} = \frac{2}{2} = 1$
$x_1 = 2~~~~\wedge~~~~x_2 = 1$
Die Funktion schneidet die x-Achse in den Punkten $N_1(1/0)$ und $N_2(2/0)$.
2. Schnittpunkte mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu berechnen, müssen wir $x=0$ einsetzen.
$x=0$
$f(0)=0^{2}-3\cdot 0+2=2$
Die Funktion schneidet die y-Achse in dem Punkt $S_y(0/2)$.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
3. Symmetrieverhalten
Der folgende Schritt in unserem Beispiel behandelt in der Kurvendiskussion die Symmetrie von Funktionen. Die Symmetrie innerhalb einer Kurvendiskussion lässt sich ohne großen Rechenaufwand bestimmen.
Methode
Methode
Hier klicken zum Ausklappen
- $f(-x) = f(x)$: achsensymmetrisch
- $f(-x) = -f(x)$: punktsymmetrisch
Achsensymmetrisch:
Wir untersuchen die Achsensymmetrie. Wir prüfen also, ob $f(-x)$ = $f(x)$ für jede reelle Zahl $x$ gilt.
$f(-x)=(-x)^{2}-3\cdot (-x) + 2 = x^2\textcolor{red}{+3x} +2$
$f(x) = x^2\textcolor{red}{-3x}+2$
Also müsste gelten: $ \textcolor{red}{3x = -3x} $. Das ist aber nur für $x$ = 0 der Fall. Die Funktion ist also nicht achsensymmetrisch.
Punktsymmetrisch:
Wir untersuchen die Punktsymmetrie. Wir prüfen also, ob $f(-x)$ = $- f(x)$ für jede reelle Zahl $x$ gilt.
$f(-x)=(-x)^{2}-3\cdot (-x)+2 = \textcolor{red}{x^2} +3x \textcolor{red}{+2} $
$- f(x)$ = $ -(x^2-3x+2)$ = $ \textcolor{red}{-x^2} + 3x \textcolor{red}{-2} $
4. Verhalten im Unendlichen
Je größer $x$ wird, desto größer werden die Funktionswerte $y$, die gegen Unendlich laufen.
$\lim_{n \to \infty}x^2-3x+2=\infty $
Werden die $x$-Werte immer kleiner, so gehen die Funktionswerte ebenfalls gegen Unendlich. Das Funktionsbild ist eine nach oben offene Parabel.
$\lim_{n \to -\infty}x^2-3x+2=\infty $
5. Monotonie und Extremwerte
Um einen Extrempunkt zu bestimmen, müssen wir die erste Ableitung bilden und diese gleich null setzen.
$f(x) = x^2-3x+2$
$f'(x) = 2x-3$
$f'(x) = 0$
$0 = 2x-3~~~~~|+3$
$3= 2x~~~~~~|:2$
$1,5 = x$
An dem x-Wert $1,5$ befindet sich ein Extrempunkt. Um zu bestimmen, ob dies ein Hoch- oder ein Tiefpunkt ist, muss die zweite Ableitung gebildet werden:
$f'(x) = 2x-3$
$f''(x) = 2 $
Nun muss der x-Wert eingesetzt werden.
Methode
Methode
Hier klicken zum Ausklappen
Ist das Ergebnis größer null, liegt ein Tiefpunkt vor. Ist das Ergebnis kleiner null, liegt ein Hochpunkt vor.
Da x in der 2. Ableitung nicht auftritt, entfällt hier in unserem Beispiel das Einsetzen des x-Wertes.
$f''(1,5) = 2 \rightarrow $ Tiefpunkt.
Nun muss noch der dazugehörige Funktionswert ermittelt werden:
$f(1,5) = 1,5^2-3\cdot 1,5+2 =- 0,25$
In dem Punkt $T(1,5/-0,25)$ befindet sich ein Tiefpunkt.
Weil der Graph eine nach oben offene quadratische Parabel ist, ist die Funktion links von Tiefpunkt monoton fallend und rechts davon monoton wachsend.
$x<1,5 \rightarrow f(x) $ ist streng monoton fallend.
6. Krümmung und Wendepunkte
Um den Wendepunkt zu bestimmen, muss die zweite Ableitung gleich null gesetzt werden.
$f''(x) = 2 $
Wird die 2=0 gesetzt, ist das eine falsche Aussage. Diese Funktion hat also keinen Wendepunkt.
Um die Krümmung zu bestimmen, gibt es eine Regel:
Methode
Methode
Hier klicken zum Ausklappen
Wir setzen für $x$ einen Wert ein und wenn gilt:
$f''(x) < 0 $ → f(x) ist an dieser Stelle rechtsgekrümmt,
Hier ist $f''(x) = 2 $ und damit ist der Funktionsgraph immer linksgekrümmt.
7. Wertebereich und Graph
Wir wissen, dass der Tiefpunkt im Punkt $T(1,5/-0,25)$ liegt und dass die Funktion kein weiteres Extremum hat. Daher können die y-Werte, die kleiner als $-0,25$ sind, nicht im Wertebereich liegen.
$W_f =[-0,25;\infty[$
Als letztes wird der Graph skizziert:
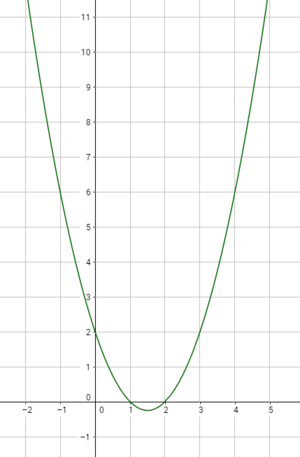
Abbildung: Graph skizzieren
Nun haben wir dir die Kurvendiskussion anhand eines Beispiels gezeigt. Teste dein neu erlerntes Wissen zum Thema Kurvendiskussion online mit unseren Übungsaufgaben. Viel Erfolg dabei!
Video: Fabian Serwitzki
Text: Chantal Rölle
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Lektor: Frank Kreuzinger
Teste dein Wissen!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
Jetzt registrieren und kostenlose Probestunde anfordern.
Dein Gratis-Lernpaket:
- Nachhilfe-Probestunden gratis
- Hausaufgaben-Soforthilfe: 15 Gratis-Minuten
- Lern-Bibliothek: 1 Tag Gratis-Zugang