Was sind senkrechte, waagerechte und schiefe Asymptoten?
Wir betrachten in diesem Lerntext Geraden, an die sich eine Funktion immer mehr annähert. Diese Geraden nennt man auch Asymptoten. Um das etwas näher zu beschreiben, haben wir einige Beispiele aufgezeichnet, damit du besser verstehst, was damit gemeint ist.
Merke
Man unterscheidet drei verschiedene Arten von Asymptoten:
- senkrechte Asymptote
- waagerechte Asymptote
- schiefe Asymptote
Senkrechte Asymptote
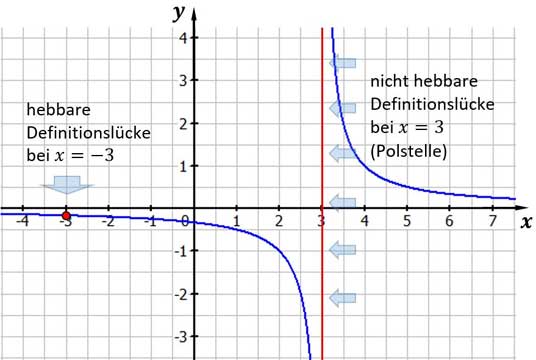
Abbildung: senkrechte Asymptote
Zu sehen ist der Graph der Funktion $f(x) =\frac{x+3}{x^2-9}$
Die Funktion ist nicht für alle Zahlen definiert. Sie besitzt dort Definitionslücken, für die der Nenner Null wird. Diese Definitionslücken befinden sich bei $x=-3$ und $x=3$. Die Lücke bei $x=-3$ ist hebbar, weil ein Punkt an dieser Stelle eingesetzt werden kann, der dann den Graphen „schließt“, also die Definitionslücke behebt. Bei $x=3$ geht das nicht, da der Sprung an dieser Definitionslücke unendlich groß ist. Diese Lücke ist also nicht hebbar. Die eingezeichnete senkrechte Gerade ist eine senkrechte Asymptote.
Das kann man mit Hilfe des Funktionsterms $f(x) =\frac{x+3}{x^2-9}$ feststellen.
Dort wird der Nenner für den $x$-Wert $3$ gleich Null, der Zähler hingegen nicht.
In diesem Fall liegt bei einer gebrochenrationalen Funktion immer eine senkrechte Asymptote vor. Diese Asymptote hat die Gleichung $x=3$
Eine senkrechte Asymptote ist keine Funktion, da sie nicht eindeutig ist.
Auch andere Funktionen besitzen senkrechte Asymptoten, zum Beispiel die Tangensfunktion.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Waagerechte Asymptote
Wie Du im folgenden Bild siehst, nähert sich der Funktionsgraph immer mehr der Gerade $y=2$ an. Das ist auch die waagerechte Asymptote. Eine Methode, eine Gleichung für diese Waagerechte zu ermitteln, ist die Grenzwertbildung. Diesen Grenzwert, den wir hier nur angeben, erhält man über sogenannte Nullfolgen. Für den Grenzwert schreibt man folgendermaßen:
$\lim_{x \to \infty}\frac{2x+10}{x-5}=2$
und liest: Limes von $\frac{2x+10}{x--5}$ für x gegen Unendlich gleich $2$.
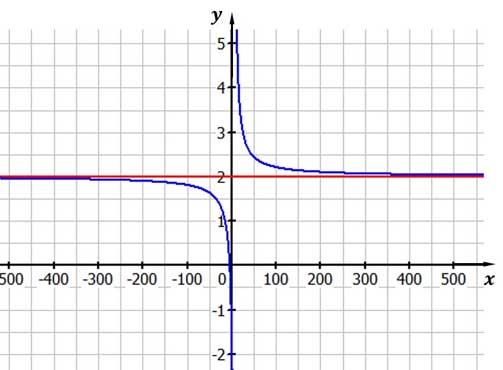
Abbildung der Funktion $f(x) =\frac{2x+10}{x-5}$ mit der Asymptote $a(x)=2$
Die Funktion, die du hier siehst hat ebenfalls eine senkrechte Asymptote bei $x=5$. Das liegt daran, dass du für x nicht 5 einsetzen darfst, denn dann ist der Nenner Null und diese Division ist ja nicht erklärt.
Die Funktion im vorherigen Abschnitt nähert sich der $x$-Achse immer weiter an. Diese Achse ist eine waagerechte Asymptote. Das siehst du in der Abbildung oben.
Schiefe Asymptoten
Wir sehen hier die Funktion ${f(x) =\frac{x^2+1}{x}}$
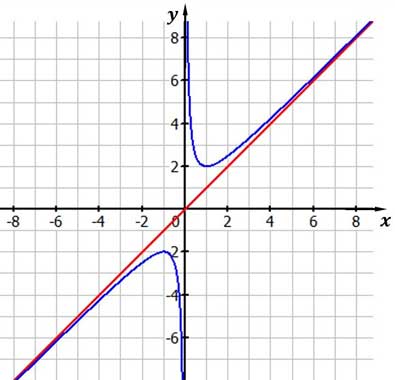
Abbildung: schiefe Asymptote
Wie du siehst, besitzt die Funktion eine schiefe Asymptote. Das ist bei einer gebrochenrationalen Funktion immer dann der Fall, wenn der Grad des Zählerpolynoms um eins höher ist als der Grad des Nennerpolynoms. Das Zählerpolynom ist quadratisch (x kommt quadratisch vor), das Nennerpolynom linear (x kommt linear vor).
Eine Gleichung der schiefen Asymptote erhält man in diesem Falle, indem man den Bruch umschreibt:
${\frac{x^2+1}{x}}={\frac{x^2}{x}}+{\frac{1}{x}}=x+{\frac{1}{x}}$
Das Ergebnis dieser Umformung besteht aus einem linearen Teil $(x)$ und einem Bruch ${\frac{1}{x}}$. Der lineare Teil stellt eine Gleichung der schiefen Asymptote dar. Es ist also: $a(x) =x$.
Die $y$-Achse ist hier ebenfalls eine Asymptote, allerdings eine senkrechte bei $x=0$. Das liegt daran, dass du für $x$ nicht Null einsetzen darfst, denn diese Division ist ja nicht erklärt.
Zusammenfassung:
Für die Asymptoten einer gebrochenrationalen Funktion ${f(x) =\frac{u(x)}{v(x)}}$ gilt:
Es gibt
…eine senkrechte Asymptote an der Stelle x, wenn der Nenner für dieses x Null ist, der Zähler dagegen nicht.
…eine waagerechte Asymptote, wenn das Zählerpolynom vom Grad her höchstens gleich dem des Nennerpolynoms ist.
…eine schiefe Asymptote, wenn das Zählerpolynom vom Grad her um genau Eins größer ist als der Grad des Nennerpolynoms.
Mit den Übungsaufgaben zu Asymptoten kannst du dein Wissen vertiefen. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Urheber: Simon Wirth, Fabian Serwitzki, Frank Kreuzinger, selbständiger Diplompädagoge, Pirna (Lektorat, fachliche Textkorrekturen und Grafikerstellung)
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
