Zahlenstrahl, Zahlengerade, Betragsfunktion einfach erklärt
Es gibt verschiedene Möglichkeiten, eine Menge an Zahlen oder einzelne Zahlen darzustellen. Hierzu zählen Zahlenstrahlen, Zahlengerade und auch Beträge von Zahlen. In diesem Text wollen wir die einzelnen Schreibweisen genauer erklären.
Zahlenstrahl
Der Zahlenstrahl ist eine der gängigsten Darstellungsformen von Zahlen. Schon in der Grundschule lernt man den Zahlenstrahl kennen und nutzt ihn für kleine Zahlen bis $10$, später bis $100$. Du kannst auch sehr gut Brüche damit kenntlich machen oder auch Verhältnisse aufzeigen. Die folgende Abbildung zeigt einen Zahlenstrahl, bei dem von $50$ Schülern in einer Klasse, genau $20$ Jungen und $30$ Mädchen sind. Also die beiden Brüche $\Large{\frac{20}{50}}$ und $\Large{\frac{30}{50}}$.
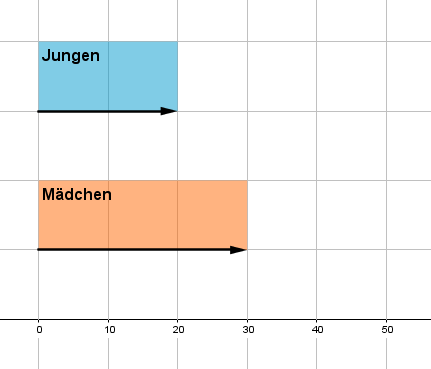
Bei der Abbildung haben wir zwei verschiedene Darstellungsmethoden verwendet. Die erste ist der Pfeil oder auch die Strecke. Diese hat die Funktion, die Anzahl zu verdeutlichen. Die zweite Variante ist ein Rechteck. Dieses veranschaulicht in unserem Beispiel das jeweilige Geschlecht. Bei der Wahl der Darstellung sind dir kaum Grenzen gesetzt, solange du erkennbar machst, welche Bedeutung dahintersteckt. Hier haben wir sowohl farblich markiert, welcher Strahl für Jungen und welcher für Mädchen steht, also auch in die Rechtecke geschrieben, worum es sich handelt.
Zahlengerade
Die Zahlengerade unterschiedet sich nur wenig vom Zahlenstrahl. So hat der Zahlenstrahl einen Anfangspunkt, die $0$. Die Zahlengerade ist, wie der Name schon andeuten lässt, eine unendlich lange Gerade, die keinen Startpunkt hat, also die negativen Zahlen beinhaltet.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beträge und Betragsfunktionen
Beträge sind eine weitere Art, wie Zahlen oder Terme in der Mathematik dargestellt werden können. Beträge zeichnen sich durch die zwei senkrechten Striche vor und hinter der Zahl oder der Gleichung aus. Beispiele hierfür sind:
$|2| \;,\; |-8|\;, \; |x+3|\;$
Das Besondere an Beträgen ist, dass die Zahl immer eine reelle nicht negative Zahl ist. Wenn du einen Betrag auflösen möchtest, dann entsteht immer eine positive Zahl. Wir schauen uns das mal an einem Beispiel an:
Beispiel
Beispiel
Löse die Gleichung:
$|x+2|=6$
Die Lösung unter dem Betrag muss also entweder $6$ oder $-6$ sein, denn der Betrag der Zahl lässt sie automatisch positiv werden. Eine Gleichung, bei der das Ergebnis negativ ist, ist daher nicht lösbar, wie zum Beispiel die folgende Gleichung:
$\textcolor{red}{|x+2|=-6}$
Um die erste Gleichung zu lösen, gehen wir die beiden möglichen Wege:
$x+2=6$ und $x+2=-6$
Wenn die Zahl unter dem Betrag also $6$ wird, dann ist die Lösung $6$. Ausgerechnet wäre $x$ also $4$. Wenn die Zahl unter dem Betrag $-6$ werden soll, muss $x$ unter dem Betrag $-8$ sein. Geschrieben wird es dann wie folgt:
$|x| := \begin{cases} \;\;\;4, & \text {für x} \ge \;{0}\\ -6, & \text{für x} < \;{0}\\ \end{cases} $
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
