Zahlenmengen: rationale, irrationale und reelle Zahlen
Mathematik und Zahlen? Das steht ja irgendwie im Zusammenhang. Es gibt bestimmte Zahlenmengen in der Mathematik. Mit drei von diesen Zahlenmengen beschäftigt sich dieser Text - mit den Zahlenmengen der rationalen Zahlen, der irrationalen Zahlen und der reellen Zahlen. Hierbei werden wir uns die Definitionen anschauen und einige Beispiele besprechen.
Gut zu wissen
Wenn du mehr über die Zahlenmenge der natürlichen Zahlen und der ganzen Zahlen erfahren möchtest, dann kannst du im Lerntext Zahlenmengen: natürliche und ganze Zahlen weiterlernen.
Rationale (gebrochene) Zahlen
Die rationalen Zahlen werden auch gebrochene Zahlen genannt, was dir bestimmt einen kleinen Hinweis gibt, welche Zahlen gemeint sein könnten: Es sind die Brüche.
Die rationalen Zahlen beinhalten neben den ganzen Zahlen auch Brüche, wie beispielsweise $ \frac{2}{3} \; oder \; \frac{3}{4}$. Hierbei ist es egal, ob der Bruch als Bruch geschrieben wird oder es sich um eine Dezimalzahl handelt, also der Bruch ausgeschrieben wurde, zum Beispiel $0,25$. Diese Zahlen gehören alle zu den rationalen Zahlen. Das Symbol der rationalen Zahlen ist das $\Large{ℚ}$.
Vertiefung
rationale Zahlen
Die Menge der rationalen Zahlen hat den Buchstaben $\Large{ℚ}$. Das kommt daher, dass die rationalen Zahlen die Brüche beinhalten und ein Bruch ja eine Division ist. Das Ergebnis solch einer Division wird in der Mathematik Quotient genannt und so lässt sich der Buchstabe Q erklären.
Merke
Rationale Zahlen sind alle ganzen Zahlen und zusätzlich alle Brüche.
Das Symbol für die rationalen Zahlen ist: $\Large{ℚ}$.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Irrationale Zahlen
Die irrationalen Zahlen sind eine weitere Menge in der Mathematik. Die irrationalen Zahlen beinhalten laut Definition nicht die rationalen Zahlen, sondern die Zahlen, die man nicht als Bruch schreiben kann. Diese Zahlen haben unendlich viele Nachkommastellen und können somit nicht als Bruch geschrieben werden. Solche Zahlen sind vor allem wichtige Konstanten, wie Pi, oder die Eulersche Zahl, aber auch die Wurzeln aus Zahlen, $\Large{\sqrt{2}}$. Diese Zahlen haben unendlich viele Nachkommastellen und können somit nicht genau bestimmt werden. Wenn du aus ihnen also eine Dezimalzahl bilden willst, musst du die Zahl runden.
Merke
Die irrationalen Zahlen sind alle Werte, die unendlich viele Nachkommastellen haben. $\Large{\sqrt{2}}$ oder die bekannte Konstante wie $\Large{π \;}$ sind Beispiele für irrationale Zahlen.
Reelle Zahlen
Die Menge der reellen Zahlen bildet keine neue Gruppe von Zahlen, sondern ist eine Summe aus den beiden Mengen, die oben erwähnt wurden, den rationalen und den irrationalen Zahlen.
Das Symbol für die reellen Zahlen ist das $\Large{ℝ}$
Merke
Die reellen Zahlen sind laut Definition alle irrationalen Zahlen und rationalen Zahlen. In ihr sind also alle wichtigen Zahlenmengen enthalten, die du für die Schule benötigst.
Das Symbol für die reellen Zahlen ist das $\Large{ℝ}$.
Reihenfolge der Zahlenmengen:
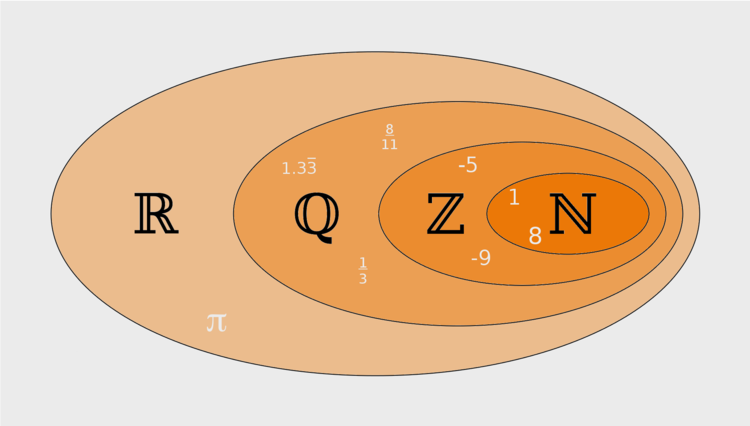
Die reellen Zahlen beinhalten die irrationalen Zahlen und die rationalen Zahlen. Die rationalen Zahlen beinhalten die ganzen Zahlen. Die ganzen Zahlen beinhalten die natürlichen Zahlen.
$\Large{ℝ \rightarrow ℚ \rightarrow ℤ \rightarrow ℕ}$
Nun weißt du mehr über rationale Zahlen, irrationale Zahlen und reelle Zahlen und hast Beispiele gesehen. Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
