Was ist ein Logarithmus?
Der Logarithmus hängt sehr stark mit dem mathematischen Begriff der Potenz zusammen. Doch wofür steht er?
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Definition eines Logarithmus
Ein Logarithmus schreibt sich wie folgt:
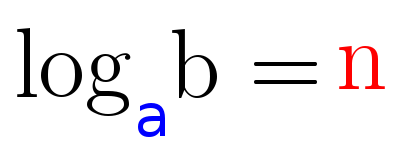
Wenn du diesen Term vorliest, hört sich das so an: Der Logarithmus von b zur Basis a ist gleich n.
Um zu verstehen, was der Logarithmus genau ausdrückt, schauen wir uns zunächst noch einmal die Potenz an:
$a^n = x$
Das sollte dir bekannt vorkommen: Die Basis a wird n-mal mit sich selbst multipliziert. Das Ziel der Berechnung einer Potenz ist dabei das Ergebnis, das sozusagen die unbekannte Komponente der Gleichung ist. Man nennt diesen Wert auch den Potenzwert.
$2^3 = x$
Merke
Bei einer Potenz fragt man nach dem Ergebnis bzw. dem Potenzwert.
Wenn du eine Potenz betrachtest, fragst du also: Was ergibt $a$ hoch $n$?
Was würdest du machen, wenn das Ergebnis und der Exponent bekannt sind und du herausfinden sollst, welchen Wert die Basis hat?
$a^3 = 8$
Tatsächlich kennst du für dieses Problem bereits eine Lösung: die Wurzel.
$\sqrt[3]{8} = a$
Merke
Bei der Wurzel fragt man nach der Basis.
Du weißt nun schon, wie man nach dem Ergebnis und der Basis fragt und ahnst wahrscheinlich schon, was jetzt kommt. Schauen wir uns folgendes Problem an:
$2^n = 8$
Hier ist der Exponent unbekannt. Die Rechnung muss so umgestellt werden, dass wir den Exponenten berechnen können: $ [...] =n$
Mit deinen jetzigen mathematischen Kenntnissen könntest du dieses Problem nicht lösen. Dank dem Logarithmus werden solche Gleichungen in Zukunft aber kein Problem mehr sein.
Der Zusammenhang zwischen einer Potenz und dem Logarithmus lässt sich also wie folgt darstellen:
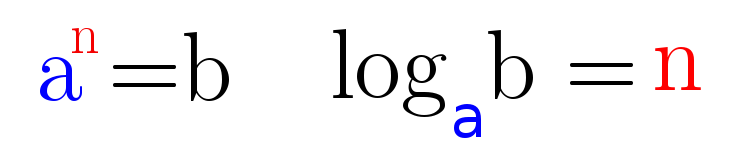
Wenn du diesen Term vorliest, hört sich das so an: Der Logarithmus von b zur Basis a ist gleich n.
Merke
Der Logarithmus gibt uns die Möglichkeit, eine Potenz nach dem Exponenten umzustellen:
$a^n = b \log_{a}(b) = n$
Beispiele für Logarithmen
Beispiel
(1) $4^3 = 64 \log_{4}(64) = 3$
(2) $3^5 = 243 \log_{3}(243) = 5$
(3) $5^{-3} = 0,008 \log_{5}(0,008) = -3$
Ihr findet auf eurem Taschenrechner eine eigene log-Taste, mit der ihr den Logarithmus problemlos berechnen könnt.
Methode
Achtung Verwechslungsgefahr!
Die Tasten log und lg haben unterschiedliche Bedeutungen. Lg beschreibt den sogenannten dekadischen Logarithmus $\log_{10}(x) = n$, bei dem die Basis immer als 10 definiert ist.
Um mit Logarithmen rechnen zu können, musst du bestimmte Rechenregeln einhalten, die du auf unserer Übersichtsseite zu den Logarithmusgesetzen findest.
Du kannst dein neu erlerntes Wissen nun noch mit unseren Übungsaufgaben testen. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
