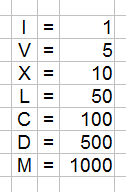Zweiersystem/Dualsystem leicht erklärt
Das Zweiersystem ist eines von vielen Zahlensystemen, das nicht nur in der Mathematik, sondern auch in der Informatik Anwendung findet. In diesem Kapitel wollen wir uns ganz dem Zweiersystem, auch Binärsystem genannt, widmen und alle Fragen dazu beantworten. Wir zeigen dir außerdem, wie du die Zahlensysteme umrechnen kannst.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Das Dualsystem
Das Dualsystem, auch Zweiersystem oder Binärsystem genannt, ist eines der wichtigsten Rechensysteme, die es gibt. Es besteht nur aus zwei Zahlen: der 0 und der 1. Es ist, wie auch das römische Zahlensystem, eine Möglichkeit, Zahlen anders darzustellen. Das heißt, es können alle Zahlen, die du kennst, auch im Binärsystem dargestellt werden. Doch wie genau stellt man Zahlen im dualen Zahlensystem dar?
Das System, was du kennst und auch in der Schule und zu Hause verwendest, nennt sich Dezimalsystem. Man hat 10 verschiedene Zahlen (0-9), die immer wieder verbunden werden und so jede erdenkliche Zahl bilden können. Das Zweiersystem kann auch jede Zahl darstellen, hat jedoch nicht 10 verschiedene Zahlen zur Verfügung, sondern muss mit zwei verschiedenen auskommen. Damit also jede Zahl gebildet werden kann, gibt es ein System. Zum besseren Verständnis schauen wir uns ein Beispiel an:
Beispiel
Verschiedene Zahlen im Binär- und im Dezimalsystem:
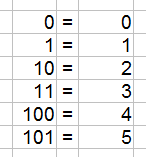
Die Basiszahlen sind $0$ und $1$. Mit jeder weiteren Stelle, die vor der Zahl hinzugefügt wird, verdoppelt sich der Zahlenwert. Sobald eine Binärzahl also 2 Stellen hat, ist sie mindestens $2$ "groß", bei 3 Stellen ist sie mindestens $4$ groß, bei einer vierstelligen Binärzahl ist der Wert mindestens $8$ und so weiter. Eine Tabelle für die Zahlensysteme mit drei Beispielzahlen findest du hier:
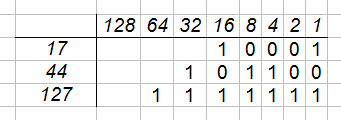
Die oberste Zeile bildet dabei eine Hilfe mit der Bedeutung der jeweiligen Stelle im Binärsystem.
Wenn du also eine Zahl aus dem Dezimalsystem ins Dualsystem umrechnest, dann hat die Zahl im Dualsystem mehr Stellen. Grundsätzlich gilt:
Je größer die Dezimalzahl, desto mehr Stellen hat auch die Binärzahl.
Dezimalzahlen in Binärzahlen umrechnen
Es gibt zwei Methoden, Dezimalzahlen in Binärzahlen umrechnen zu können.
Methode 1
Die erste Methode benötigt eine Binärsystemtabelle, wie bei den drei Beispielzahlen oben. Wenn du dann eine Zahl umwandeln willst, etwa die $44$, dann schaust du, welche Zahlen du aus dem Zweiersystem benötigst und fügst sie zusammen. Im Beispiel also $1 \cdot 32 + 0\cdot 16 + 1 \cdot 8 + 1 \cdot 4 + 0 \cdot 2 + 0 \cdot 1$. Wichtig sind auch die Nullen, denn ohne die Nullen ergibt sich nicht $44$, sondern $7$.
Aufgeschrieben ergibt sich für $44$ im Binärsystem dann die Zahl $101100$.
Methode 2
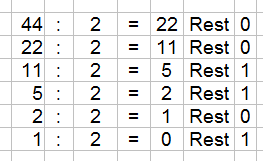
Wir dividieren die Dezimalzahl durch $2$. Die Ergebnisse werden so lange weiter durch zwei geteilt, bis die Lösung Null ist. Der Rest ist dann die entscheidende Zahl, denn daraus entsteht die Dualzahl: $101100$ .
Binärzahlen umrechnen in Dezimalzahlen
Um Binärzahlenumrechnen zu können und das in Dezimalzahlen, gehst du die einzelnen Stellen der Dualzahl ab und addierst dort wo eine $1$ steht jeweils die Zahlen. Dann entsteht die gesuchte Dezimalzahl:
$10101 = 1 \cdot 16 + 0 \cdot 8 + 1 \cdot 4 + 0 \cdot 2 + 1 \cdot 1 = 21$
Du suchst nun zu diesem binären bzw. dualen Zahlensystem Übungen? Zur Vertiefung des Zweiersystems schau einmal in die Übungsaufgaben! Viel Spaß dabei!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema