Schriftliche Multiplikation - Aufgaben und Einführung
In diesem Kapitel befassen wir uns mit der schriftlichen Multiplikation. Dies ist eine einfache Methode, mit der du multiplizieren kannst, ohne Taschenrechner.
Du suchst zum Thema schriftliche Multiplikation Aufgaben, damit du fit im schriftlichen Multiplizieren wirst? Im Folgenden werden wir mit dir ein Beispiel zur schriftlichen Multiplikation durchrechnen und dir die Regeln für das schriftliche Multiplizieren erklären.
Gut zu wissen
Die Grundlage für dieses Kapitel bildet das Wissen über die Multiplikation.
In 4 Schritten 2 Zahlen miteinander schriftlich multiplizieren
Im Folgenden ist die Vorgehensweise aufgeführt, wie du ohne Taschenrechner zwei Zahlen miteinander schriftlich multiplizierst. Zuallererst schreibst du die zwei Zahlen, die du multiplizieren willst, nebeneinander und setzt einen Mal-Punkt dazwischen. Anschließend gehst du wie folgt vor:
Methode
- Multipliziere die erste Ziffer des rechten Faktors mit dem gesamten linken Faktor. Das Ergebnis schreibst du unter die erste Ziffer des rechten Faktors.
- Multipliziere die zweite Ziffer des rechten Faktors mit dem gesamten linken Faktor. Das Ergebnis schreibst du unter die zweite Ziffer des rechten Faktors.
- Multipliziere die dritte Ziffer des rechten Faktors mit dem gesamten linken Faktor. Das Ergebnis schreibst du unter die dritte Ziffer des rechten Faktors. So gehst du beliebig vor, je nachdem, wie viele Ziffern du in deinem rechten Faktor hast.
- Addiere die Ergebnisse der letzten Schritte von rechts nach links zusammen (siehe am Ende der nächsten Beispiel-Box).
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Schriftliche Multiplikation
Du kennst bereits die Multiplikation. Die schriftliche Multiplikation unterscheidet sich nicht von der Multiplikation, sondern bildet eine Methode, wie du große Zahlen ohne Taschenrechner einfach multiplizieren kannst. Schauen wir uns hierzu ein Beispiel an:
Beispiel
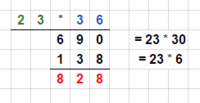
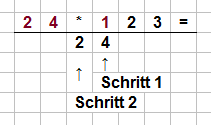
Aufgabenstellung: Multipliziere $24$ mit $123$.
Der erste Schritt ist das Nebeneinanderschreiben:
$24 \; \cdot \; 123 \; =$
Jetzt folgt das Errechnen. Dazu multiplizieren wir im ersten Schritt die erste Ziffer des zweiten Faktors, also die $1$ von der Zahl $123$, mit den Ziffern der ersten Zahl. Erst $1 \; \cdot \; 4$, was $4$ ergibt. Diese Zahl schreiben wir direkt unter die $1$. Danach multiplizieren wir die $1$ mit der $2$ und erhalten $2$. Diese Zahl stellen wir vor die $4$.
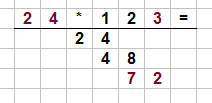
Der zweite große Schritt bei der schriftlichen Multiplikation ist die Multiplikation der zweiten Ziffer des zweiten Faktors, also die $2$, mit der $24$. Wir gehen wie im ersten Schritt vor und erhalten:
$24 \; \cdot \; 2 \; = \; 48$.
Dieses Mal schreiben wir die Zahl unter die $2$ und erhalten:

Im dritten Schritt rechnen wir die $3$ mal die $24$ und erhalten $72$. Diese Zahl schreiben wir unter die drei und es entsteht insgesamt:
Der vierte und letzte Schritt ist das schriftliche Addieren der einzelnen Werte. Hierbei addieren wir jedoch nicht $24$ mit $48$ und $72$. Die Position der Zahlen spielt hierbei eine wichtige Rolle. Denn eigentlich haben wir im ersten Schritt nicht $24 \; \cdot \; 1$ gerechnet, sondern $24 \; \cdot \; 100$ und auch im zweiten Schritt haben wir nicht $24 \; \cdot \; 2$, sondern $24 \; \cdot \; 20$ gerechnet.
Das Ergebnis dieser Rechnung siehst du in der folgenden Abbildung:
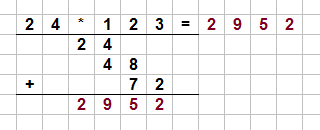
Schriftliche Multiplikation - Regeln
Merke
Das schriftliche Multiplizieren ist eine Methode zum einfacheren Multiplizieren größerer Zahlen.
Multipliziere die Ziffern des zweiten Faktors einzeln mit dem ersten Faktor. Danach addierst du die einzelnen Werte und erhältst die Lösung.
Alles klar? Zur Vertiefung dieses Themas schau dir auch noch einmal die Aufgaben zur schriftlichen Multiplikation an. Viel Erfolg dabei!
Teste dein Wissen!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema