Prozent in Brüche oder Dezimalzahlen umrechnen
Prozente sind dir bestimmt schon oft begegnet. Doch was steckt mathematisch eigentlich hinter diesem $\%$ Zeichen und wie kann man damit rechnen?
4 Fakten über Prozentrechnung
Wir haben dir hier schon mal das Wichtigste über das Umrechnen von Prozentangaben in Brüche oder Dezimalzahlen aufgelistet:
Methode
- $100 \%$ entspricht dem Ganzen.
- Prozentangaben kannst du in Brüche umwandeln: $\% = \frac{1}{100}$
- Dezimalzahlen und die natürliche Zahl $1$ kannst du in Prozente umrechnen, indem du diese mit 100 multiplizierst.
- Den Relativen Anteil von etwas Ganzem berechnest du wie folgt: $\frac{Anteil}{Ganze}$. Das Ergebnis musst du danach dann einfach nur noch in eine Prozentangabe umrechnen.
Im Folgenden erklären wir dir diese Informationen nun detaillierter und geben dir Beispiele an die Hand.
Bedeutung von Prozent: Teile eines Ganzen
Eine Prozentangabe gibt normalerweise den Teil eines Ganzen an. Wir beschreiben also das Verhältnis von etwas Kleinerem zu etwas Größerem. Dabei entspricht das Ganze immer $100\%$.
Beispiel
Du möchtest herausfinden, welcher Anteil einer Schulklasse Mädchen sind und welcher Jungen. Insgesamt sind 26 Schüler in der Klasse. Somit entsprechen die 26 Schüler den $100\%$. Durch Abzählen findest du heraus, dass in der Klasse 13 Mädchen sind, also genau die Hälfte. Es sind also $50\%$ Mädchen in der Klasse.
Wie du siehst, hat die Zahl 100 nicht unbedingt etwas mit dem Sachverhalt zu tun, den du untersuchst. Völlig egal, ob du eine Schulklasse mit 15, 24, 35 oder 40 Schülern betrachtest - die gesamte Klasse entspricht immer $100 \%$. Genauso entspricht die Hälfte der jeweiligen Klasse immer $50\%$, egal wie viele Schüler das tatsächlich sind.
Dieses grundlegende Prinzip solltest du immer im Hinterkopf haben.
Prozente in Brüche umrechnen
Wie gehen wir in der Mathematik mit Prozenten um? Du hast schon gelernt, dass Prozente Teile eines Ganzen ausdrücken. Diese Formulierung kennst du vielleicht schon von einem anderen Thema deines Matheunterrichts: der Bruchrechnung. Die Prozent-Zeichen lassen sich nämlich auch als Brüche ausdrücken:
$\% = \frac{1}{100}$
Allgemein gilt demnach: ${\textcolor{red}{z}} \% = {\frac{\textcolor{red}{z}}{100}}$
So kannst du jede Prozentangabe in einen Bruch umwandeln. Du musst hier jedoch beachten, dass du an manchen Stellen die Brüche noch kürzen kannst.
Beispiel
$60 \% = \frac{60}{100} = \frac{60:20}{100:20} = \frac{3}{5}$
Der Zähler und der Nenner von dem Bruch $\frac{60}{100}$ haben den gemeinsamen Teiler $20$. Deswegen dividierst du Zähler und Nenner durch $20$. So ergibt sich das gekürzte Ergebnis $\frac{3}{5}$.
Wenn du dir beim Kürzen von Brüchen noch unsicher bist oder nochmal nachlesen willst, wie das Kürzen von Brüchen funktioniert, dann lies doch im Lerntext zum Thema Brüche kürzen und erweitern nach.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Prozente in Dezimalzahlen umrechnen
Merke
Das Prozentzeichen gibt an, dass die Zahl jeweils mit $\frac{1}{100}$ multipliziert werden muss:
- $100 \% = 100 \cdot \frac{1}{100} = \frac{100}{100} = 1$
- $80 \% = 80 \cdot \frac{1}{100} = \frac{80}{100} = 0,8$
- $10\% = 10 \cdot \frac{1}{100} = \frac{10}{100} = 0,1$
- $1\% = 1 \cdot \frac{1}{100} = \frac{1}{100} = 0,01$
Jetzt haben wir aus den Prozentangaben Dezimalzahlen gemacht, mit denen sich viel besser rechnen lässt. Aber auch bei der Dezimal-Schreibweise geht es immer noch um Anteile an einem Ganzen. Das Ganze entspricht nun jedoch nicht mehr $100\%$, sondern der Zahl $1$.
Du kannst natürlich auch Dezimalzahlen in Prozente umrechnen, indem du einfach mit 100 multiplizierst.
- $1 \cdot 100 = 100 \%$
- $0,99 \cdot 100 = 99\%$
- $0,03 \cdot 100 = 3 \%$
Merke
Rechnest du eine Prozentangabe in eine Dezimalzahl um, so verschiebst du das Komma um 2 Stellen nach links.
Rechnest du eine Dezimalzahl in eine Prozentangabe um, so verschiebst du das Komma um 2 Stellen nach rechts. Hinter das Ergebnis schreibst du einfach das Prozentzeichen.
Gut zu wissen
Woher kommt der Begriff Prozent?
Die Bezeichnung Prozent leitet sich vom italienischen per cento ab, was von Hundert bedeutet. Daraus hat sich in Deutschland im Laufe der Zeit pro cento entwickelt. Pro kommt aus dem Lateinischen und bedeutet dasselbe wie das italienische per.
Eine große Verwechslungsgefahr besteht mit dem Begriff Promille, der sich ebenfalls vom italienischen ableiten lässt und von Tausend bedeutet.
Rechnen mit Prozentangaben
Mithilfe der Umrechnung einer Prozentangabe in die entsprechende Dezimalzahl können wir herausfinden, wie viel eines Ganzen einer bestimmten Prozentangabe entspricht. Dazu musst du einfach den Wert des Ganzen mit der entsprechenden Prozentzahl (in der Dezimal-Schreibweise) multiplizieren.
Beispiel
Von Prozent auf den Anteil
Bei einer Mathearbeit haben $25 \%$ der Schüler eine Zwei geschrieben. Insgesamt haben 24 Schüler an der Mathearbeit teilgenommen. Wie viele Schüler haben eine Zwei geschrieben?
$24$ Schüler $\cdot~25 \% = 24 \cdot (25 \cdot \frac{1}{100}) = 24 \cdot 0,25 = 6$
$25\%$ von 24 Schülern entsprechen 6 Schülern.
6 Schüler haben in der Mathearbeit eine Zwei geschrieben.
Etwas schwieriger wird es, wenn du herausfinden möchtest, wie viel Prozent einer bestimmten Anzahl an Schülern entsprechen. In diesem Fall berechnest du erst das Verhältnis zwischen dem Anteil und dem Ganzen als Dezimalzahl und wandelst diese dann in Prozent um.
Das Verhältnis zwischen Anteil und Ganzem berechnest du, indem du den Anteil durch das Ganze dividierst. Man nennt dies auch den relativen Anteil:
Merke
$Verhältnis\ des\ Anteils\ zum\ Ganzen = \frac{Anteil}{Ganze}$
Der relative Anteil kann nur zwischen null und eins liegen.
Beispiel
Vom Anteil auf Prozent
Bei der Mathearbeit haben 3 Schüler eine Drei geschrieben. Es haben insgesamt 24 Schüler an der Mathearbeit teilgenommen. Wie viel Prozent der Schüler haben eine Drei geschrieben?
$Relativer\ Anteil : \frac {3\ Schüler}{24\ Schüler} = 0,125$
Wenn du den relativen Anteil kennst, kannst du die Dezimalzahl in Prozent umrechnen:
$0,125 \cdot 100 = 12,5 \%$
$12,5 \%$ der Schüler haben eine Drei geschrieben.
In den Übungsaufgaben kannst du nun dein neues Wissen zur Umrechnung von Prozenten testen. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
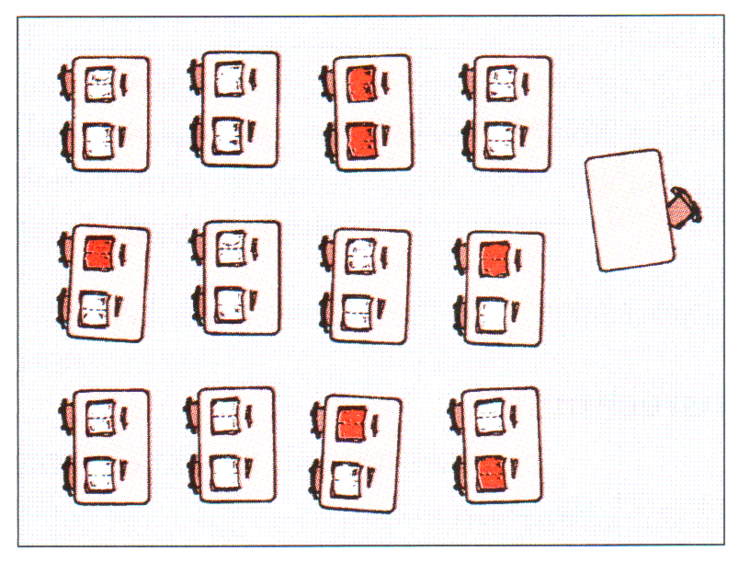
Die Abbildung zeigt eine Schulklasse von oben. Die roten Hefte gehören Schülern, die eine Fünf oder eine Sechs geschrieben haben. Die weißen Hefte gehören Schülern, die eine bessere Note geschrieben haben.
Wie viel Prozent der Schüler haben eine Fünf oder eine Sechs in der Klassenarbeit geschrieben?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
