Grundbegriffe der Wahrscheinlichkeitsrechnung
Ein Teilgebiet der Mathematik ist die Stochastik. Du wirst diesen Begriff eher als Wahrscheinlichkeitsrechnung oder Wahrscheinlichkeitsberechnung kennenlernen. Wenn du dich in Mathe mit Wahrscheinlichkeitsrechnung beschäftigst, begegnest du sicher oft der Frage, wie wahrscheinlich das Eintreffen bestimmter Ereignisse ist. Ein zentraler Bestandteil dieser mathematischen Disziplin ist der Umgang mit Prozentangaben. Hinzu kommen einige neue Grundbegriffe, die wir im Folgenden besprechen werden.
Ergebnis und Ereignis
Das Ergebnis und das Ereignis werden in der Wahrscheinlichkeitsrechnung oft miteinander verwechselt. Daher ist es wichtig, den genauen Unterschied zwischen diesen beiden Begriffen zu kennen. Um diesen Unterschied besser zu verstehen, nutzen wir als Beispiel das Werfen eines Würfels.
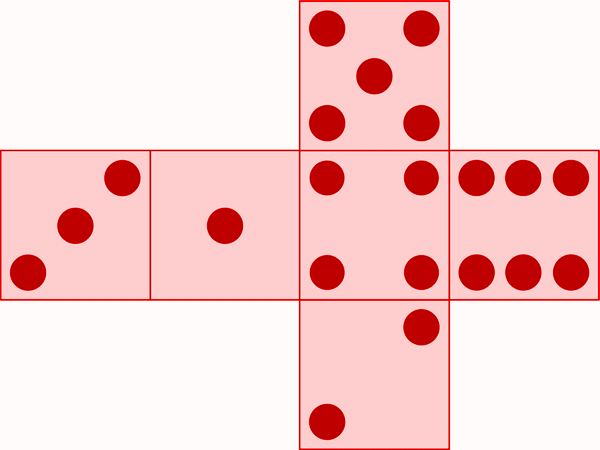
Der Wurf des Würfels kann zu 6 möglichen Ausgängen führen. Jeder einzelne dieser Ausgänge stellt ein Ergebnis dar. Diese 6 möglichen Ergebnisse (1, 2, 3, 4, 5 und 6) fasst man in der Stochastik zusammen zur Ergebnismenge.
Beispiel
Beispiel
Ergebnismenge (einmaliges Würfeln): Ω = {1; 2; 3; 4; 5; 6}
Das Ergebnis leitet sich also vom Versuchsgegenstand, in diesem Fall dem Würfel, ab und hat noch nichts damit zu tun, wie wahrscheinlich etwa das Würfeln einer bestimmten Zahl ist. Egal welches Zufallsexperiment wir mit diesem Würfel durchführen - die Ergebnismenge bleibt immer gleich.
Ein Ereignis ist eine Teilmenge der Ergebnismenge. Ein Ereignis kann aus einem einzelnen Ergebnis oder aus mehreren Ergebnissen bestehen. Je nachdem was wir untersuchen, ändert sich also das Ereignis, auch wenn der Gegenstand der Untersuchung (Würfel) gleich bleibt.
Die Wahrscheinlichkeit für das Eintreten eines bestimmten Ereignisses kürzt man wie folgt ab: $P\ (E)$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Wahrscheinlichkeitsrechnung - Beispiele
Im Lernvideo haben wir dir bereits einen kleinen Einblick in die Wahrscheinlichkeitsrechnung gegeben. Im Folgenden findest du zwei weitere Beispiele zu Wahrscheinlichkeiten beim Würfeln, die wir dir schriftlich vorrechnen:
Beispiel 1
Beispiel
Beispiel
Ereignis: Wie wahrscheinlich ist es, eine $3$ zu würfeln?
Ereignismenge: $E = \{3\}$
Wahrscheinlichkeit: $P(E) = P(3) = \frac{1}{6}$
Beispiel 2
Beispiel
Beispiel
Ein Ereignis kann auch aus mehreren Ergebnissen bestehen: Wie wahrscheinlich ist es, eine $2$ oder eine $3$ zu würfeln?
Ereignismenge: $E = \{2; 3\}$
Wahrscheinlichkeit: $P(E) = \frac{2}{6} = \frac{1}{3}$
Es gibt natürlich auch die Möglichkeit, dass Ergebnismenge und Ereignismenge übereinstimmen. In unserem Beispiel wäre dies das Ereignis: Wie wahrscheinlich ist es, eine 1, 2, 3, 4, 5 oder 6 zu würfeln? Da dieses Ereignis alle Ergebnisse beinhaltet, die eintreffen können, nennt man es auch das sichere Ereignis.
Merke
Merke
- Die Ergebnismenge enthält alle Ergebnisse, die eintreten können.
- Ein Ereignis besteht aus Elementen der Ergebnismenge. Das heißt, ein Ereignis ist eine Teilmenge der Ergebnismenge.
- Wenn ein Ereignis alle Elemente der Ergebnismenge beinhaltet, bezeichnet man das Ereignis als sicheres Ereignis. Ergebnismenge und Ereignismenge sind dann identisch.
Umgang mit Wahrscheinlichkeiten
Für einen sicheren Umgang mit Wahrscheinlichkeiten in Mathe sind Kenntnisse im Bereich der Prozentrechnung sehr wichtig. Du solltest den Zusammenhang von Dezimalzahlen und Prozentangaben verstanden haben und in der Lage sein, Brüche in Dezimalzahlen und in Prozentangaben umzurechnen, und umgekehrt.
Die Wahrscheinlichkeit beim einmaligen Werfen eine bestimmte Zahl zu würfeln, ist für jede Zahl gleich und berechnet sich über den relativen Anteil (die relative Häufigkeit):
$relativer\ Anteil = \frac{Anteil(e)}{Ganze} = \frac {1}{6} ~\approx ~0,17 ~ \widehat{=}~16~\%$
Wenn du dich in diesem Bereich noch nicht fit fühlst, solltest du dich noch einmal mit unserem Lerntext zu diesem Thema beschäftigen.
Gegenereignis
Ein Gegenereignis enthält alle Ergebnisse, die nicht zum Ereignis zählen. Gegenereignis und Ereignis sind also zusammengenommen dasselbe wie die Ergebnismenge, nämlich alle Ergebnisse, die überhaupt eintreten können. Viel wichtiger als dieser Zusammenhang ist aber, dass die Summe der Wahrscheinlichkeiten von Ereignis und Gegenereignis immer 1 bzw. 100 % ergeben muss.
Beispiel
Beispiel
Die Wahrscheinlichkeit eine 1 zu Würfeln beträgt $\frac{1}{6}$.
Das Gegenereignis $\overline {E}$ deckt nun alle anderen Ergebnisse ab, die nicht zum Ereignis $E$ gehören; also, das Würfeln einer 2, 3, 4, 5 oder 6.
Da die Summe von Ereignis und Gegenereignis immer 1 ergeben muss, können wir die Wahrscheinlichkeit des Gegenereignisses berechnen:
$P (\overline {E}) = 1 - P (E) = 1 - \frac {1}{6} = \frac {5}{6} \approx 0,83 ~\widehat{=} ~83~\%$
In den Übungsaufgaben kannst du jetzt dein Wissen über die Wahrscheinlichkeitsrechnung testen. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Du würfelst einmal und betrachtest das Ereignis "eine 2 oder eine 4 würfeln".
Wie lautet das Gegenereignis $\overline{E}$?
Du ziehst aus einem Behälter mit einer weißen, einer blauen und einer roten Kugel eine Kugel heraus.
Wie lautet die Ergebnismenge Ω dieses Zufallsversuches?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
