Laplace Experiment: Regel, Beispiele, Aufgaben
In diesem Lerntext erklären wir dir alles zum Thema Laplace-Experimente, eine Art von Zufallsexperimenten, die du aus deinem Mathematikunterricht schon kennen wirst. Du wirst schnell verstehen, wie du bei dieser Art von Zufallsversuchen rechnest. Am Ende kannst du dein erlerntes Wissen zu Laplace und Wahrscheinlichkeiten in Aufgaben weiter vertiefen und kontrollieren.
Laplace Experiment - Definition
Ein Laplace Experiment ist eigentlich nichts anderes als das, was du in deinem Matheunterricht als Zufallsversuch kennenlernst - mit einer kleinen Einschränkung: Ein Laplace Experiment ist ein Zufallsversuch, bei dem die Wahrscheinlichkeiten aller möglichen Ergebnisse gleich sind. Typische Beispiele bei Laplace sind in der Regel das Werfen einer Münze oder eines gewöhnlichen Würfels. Das Besondere an diesen Versuchen ist, dass sie uns das Rechnen mit Wahrscheinlichkeiten vereinfachen. In Laplace-Experimenten gilt die Regel:
$P (E) = \frac {Anzahl\ der\ gewünschten\ Ergebnisse}{Anzahl\ der\ möglichen\ Ergebnisse}$
Wir müssen also einfach die Anzahl der Ergebnisse, die gewünscht sind, durch die Anzahl aller Ergebnisse dividieren.
Merke
Merke
Ein Laplace Experiment ist ein Zufallsversuch, bei dem die Wahrscheinlichkeiten aller möglichen Ergebnisse gleich sind.
Es gilt:
$P (E) = \frac {Anzahl\ der\ gewünschten\ Ergebnisse}{Anzahl\ der\ möglichen\ Ergebnisse}$
Wie du siehst, ist die Rechnung für dich nicht neu. Und das ist nicht verwunderlich, da die allermeisten Zufallsexperimente, die du bis jetzt kennengelernt hast, Laplace-Experimente sind. Im Lerntext Zufallsversuche - Wahrscheinlichkeit von Ergebnissen berechnen kannst du nochmal alles Weitere dazu nachlesen.
Gut zu wissen
Hinweis
Pierre-Simon Laplace war ein französischer Mathematiker und Physiker, der um 1800 zu den Themen Wahrscheinlichkeitsrechnung und Differentialgleichungen forschte. Der Name Laplace kann dir in deinem Mathematikunterricht noch öfter begegnen.
Betrachten wir nun einige Beispiele, um den Unterschied zwischen Laplace-Experimenten und anderen Zufallsversuchen zu verstehen.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispiele für Laplace Experimente
Beispiel 1
Das erste "Laplace-Beispiel" ist ein wirklicher Klassiker in der Wahrscheinlichkeitsrechnung: das einmalige Werfen eines Würfels. Ein normaler Würfel hat sechs Seiten, die mit den Zahlen 1 bis 6 beschriftet sind. Jede Zahl hat die gleiche Wahrscheinlichkeit, gewürfelt zu werden.
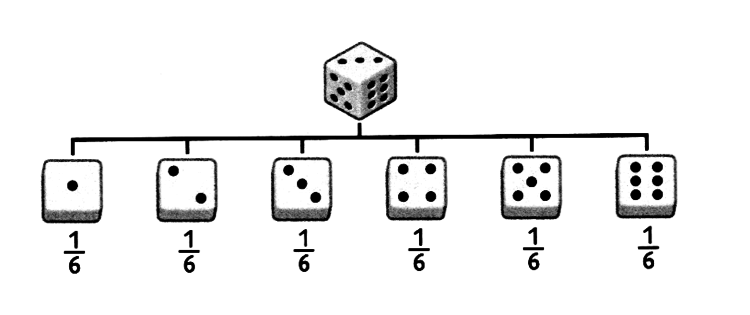
Jede Zahl wird mit einer Wahrscheinlichkeit von
$P(E) = \frac {1}{6} \approx 16,7 \%$
gewürfelt.
Betrachten wir die Wahrscheinlichkeit für das Ereignis "eine gerade Zahl würfeln":
Ereignis: "eine gerade Zahl würfeln"
Ereignismenge: $E= \{2, 4, 6\}$
$P (E) = \frac {3}{6} = \frac {1}{2}~~\widehat{=}~~50 \%$
Weitere Beispiele
Im folgenden Beispielkasten siehst du noch zwei weitere Beispiele, die dir beim Thema Laplace in Wahrscheinlichkeitsrechnung in Mathe begegnen können:
Beispiel
Beispiel
- Das Werfen einer Münze: Die Wahrscheinlichkeit für Kopf und Zahl liegt jeweils bei $50 \%$
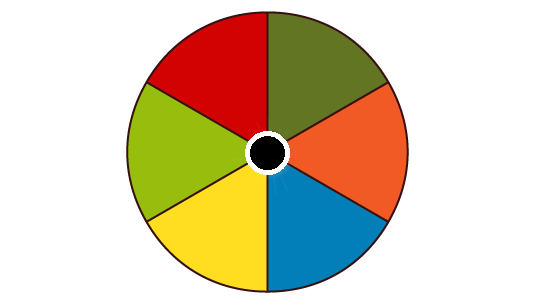
- Das Drehen dieses Glücksrades: Jedes Feld hat eine Wahrscheinlichkeit von $ \frac {1}{6} \approx 16,7 \%$
Was sind keine Laplace-Aufgaben?
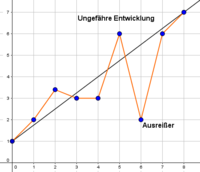
Schauen wir uns einmal an, welche Art von Zufallsversuch kein Laplace-Experiment ist. Es gibt einige Zufallsversuche, bei denen nicht alle möglichen Ergebnisse die gleiche Wahrscheinlichkeit haben.
Dazu gehören beispielsweise Würfel, bei denen eine bestimmte Zahl auf mehr als einer Seite abgebildet ist oder das Werfen einer Reißzwecke, die auf Grund ihrer Form nicht auf jeder Seite gleich wahrscheinlich liegen bleibt.
Nun weißt du, was ein Laplace-Experiment in Mathe ist, welche Regeln bei Laplace gelten und wie du die jeweiligen Wahrscheinlichkeiten bestimmen kannst. Vertiefe dein Wissen zu Laplace und Wahrscheinlichkeit in unseren Aufgaben. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Weitere Erklärungen & Übungen zum Thema
Hol dir Hilfe beim Studienkreis und frag einen Lehrer!
Du benötigst Hilfe bei einer Aufgabe? Nutze die Mathematik-Hausaufgabenhilfe und bespreche deine Aufgabe sofort ohne Termin per Online-Chat mit einem Mathematik-Lehrer.
- Sofort, ohne Termin
- Online-Chat 14 – 20 Uhr
- Erfahrene Mathematik-Lehrer
Du benötigst häufiger Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik Online-Nachhilfe und verbessere deine Mathematik-Kenntnisse.
- Zum Wunschtermin
- Online-Einzelgespräch
- Geprüfte Nachhilfelehrer
Du möchtest lieber einen Lehrer der Mathematik-Nachhilfe aus deiner Stadt im persönlichen und direkten Gespräch fragen? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Zum Wunschtermin
- In deiner Stadt
- Geprüfte Nachhilfelehrer
- Nachhilfe Berlin
- Nachhilfe München
- Nachhilfe Nürnberg
- Nachhilfe Köln
- Nachhilfe Düsseldorf
- Nachhilfe Dortmund
- Nachhilfe Hamburg
- Nachhilfe Hannover
- Nachhilfe Bremen
- Nachhilfe Leipzig
- Nachhilfe Dresden
Standort nicht gefunden? Rund 1000 Nachhilfe-Standorte bundesweit!
Nachhilfe gesucht
Du möchtest mehr Aufgaben? Zugriff auf alle Aufgaben erhältst du im Studienkreis Lernportal.
- Über 250.000 Übungsaufgaben
- 700 Lernvideos
- Original-Abi-Klausuren
Unsere Kunden über den Studienkreis
Wir sind durchgehend für dich erreichbar
Jetzt registrieren und kostenlose Probestunde anfordern.
Dein Gratis-Lernpaket:
- Nachhilfe-Probestunden gratis
- Hausaufgaben-Soforthilfe: 15 Gratis-Minuten
- Lern-Bibliothek: 1 Tag Gratis-Zugang