In Mathe in der Kombinatorik, einem Teilgebiet der Stochastik, geht es um die Bestimmung der Anzahl möglicher Anordnungen oder Auswahlen von Objekten.
Je nachdem, ob man unterschiedliche Anordnungen, Auswahlmöglichkeiten oder beides berechnen möchte, gibt es verschiedene Rechenoperationen. Um zu entscheiden, welche Berechnung man für eine bestimmte Aufgabe benötigt, hilft folgender Entscheidungsbaum:
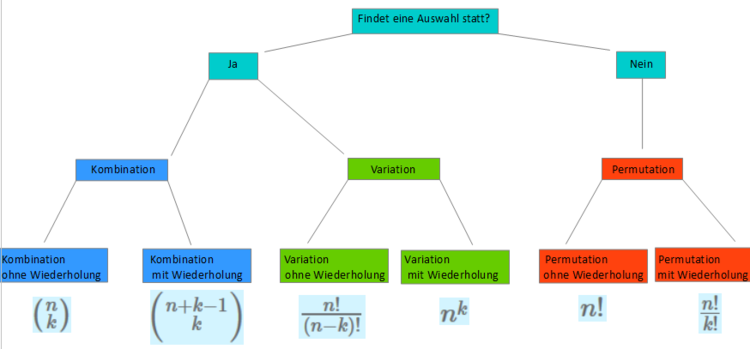
Im Folgenden gehen wir die verschieden Berechnungsmöglichkeiten durch und zeigen dir die Varianten der Kombinatorik an verschiedenen Beispielen und Aufgaben.
1. Möglichkeit: Es wird keine Auswahl getroffen
Zunächst müssen wir uns fragen, ob in der Aufgabenstellung von einer Auswahl an Objekten die Rede ist oder die Gesamtmenge der Objekte gemeint ist (= keine Auswahl).
Wird keine Auswahl getroffen, so berechnen wir die verschiedenen Anordnungsmöglichkeiten der Objekte mithilfe der Permutation. Dabei unterschiedet man eine Menge an Objekten, die alle unterscheidbar sind (= Permutation ohne Wiederholung) und eine Menge an Objekten, die teilweise nicht voneinander zu unterscheiden sind (= Permutation mit Wiederholung).
Permutation ohne Wiederholung
Merke
Um die Anzahl verschiedener Kombinationsmöglichkeiten von $n$ unterscheidbaren Objekten zu berechnen, rechnet man:
$\Large{n!}$
Beispiel
In einer Urne befinden sich sechs verschiedenfarbige Kugeln. Wie viele Möglichkeiten gibt es, die Kugeln in einer Reihe anzuordnen?
$n~=~6$
$n!~=~1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6~=~720$
Es gibt insgesamt 720 Möglichkeiten.
Permutation mit Wiederholung
Merke
Die Anzahl der Kombinationsmöglichkeiten von $n$ Objekten, von denen $k$ Objekte identisch sind, berechnet sich durch:
$\Large{\frac{n!}{k!}}$
Sind mehrere Objekte identisch, gilt:
$\Large{\frac{n!}{k_1! \cdot k_2!...}}$
Beispiel
In einer Urne befinden sich drei grüne und zwei gelbe Kugeln. Wie viele Möglichkeiten gibt es, die Kugeln in einer Reihe zu ordnen?
$\Large{\frac{n!}{k!}~=~\frac{5!}{3! \cdot 2!}~=~\frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5}{(1\cdot 2 \cdot 3) \cdot (1\cdot 2)}~=~\frac{120}{12}~=~10}$
Es gibt $10$ Möglichkeiten.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
2. Möglichkeit: Es wird eine Auswahl getroffen
Wird eine Auswahl von Objekten aus einer Gesamtmenge getroffen, berechnen wir die Kombination oder die Variation. Die Permutation hilft uns in diesem Fall nicht weiter.
Die Kombination gibt die Anzahl der Möglichkeiten an, eine bestimmte Menge an Objekten aus einer größeren Gesamtmenge auszuwählen.
Die Variation gibt an, wie viele Möglichkeiten existieren, eine bestimme Auswahl an Objekten zu ordnen. Die Variation berücksichtigt also zwei Dinge: Zum einen gibt es verschiedene Möglichkeiten, eine Auswahl zu treffen. Zum anderen kann diese Auswahl unterschiedlich geordnet werden.
Kombination ohne Wiederholung
Merke
Um zu berechnen, wie viele Möglichkeiten es gibt, $k$ Objekte aus einer Gesamtmenge von $n$ Objekten auszuwählen, rechnet man:
$\Large{\binom{n}{k}}$
Gesprochen: "n über k" oder "k aus n"
Beispiel
Beim Lotto werden sechs Zahlen aus insgesamt $49$ gewählt. Wie viele Möglichkeiten gibt es? Du kannst die Kombinationen so berechnen:
Anzahl der ausgewählten Objekte $k~=~6$
Anzahl der Gesamtmenge an Objekten $n~=~49$
Berechnung der Kombination: $\Large{\binom{n}{k}~=~ \binom{49}{6}}~=~13.983.816$
Es existieren 13.983.816 (fast 14 Millionen) Auswahlmöglichkeiten.
Kombination mit Wiederholung
Merke
Um zu berechnen, wie viele Möglichkeiten es gibt $k$ Objekte aus einer Gesamtmenge von $n$ Objekten auszuwählen, wobei die Objekte mehrmals ausgewählt werden dürfen, rechnet man:
$\Large{\binom{n + k - 1}{k}}$
Beispiel
In einem Gefäß befinden sich sechs verschiedenfarbige Kugeln. Es werden drei der Kugeln gezogen, wobei die gezogene Kugel nach jedem Zug wieder zurückgelegt wird (= mit Wiederholung).
Anzahl der ausgewählten Objekte $k~=~3$
Anzahl der Gesamtmenge an Objekten $n~=~6$
Berechnung der Kombination: $\Large{\binom{n + k - 1}{k}~=~ \binom{6 + 3 - 1}{3}~=~ \binom{8}{3}}~=~56$
Es existieren 56 Auswahlmöglichkeiten.
Variation ohne Wiederholung
Merke
Um die Anzahl von Kombinationsmöglichkeiten einer Auswahl von $k$ Objekten von einer Gesamtanzahl an $n$ Objekten zu berechnen, benutzen wir folgende Formel:
$\Large {\frac{n!}{(n - k)!}}$
Beispiel
In einer Kiste befinden sich sechs verschiedenfarbige Kugeln, von denen vier Kugeln gezogen werden. Wie viele Möglichkeiten gibt es, die Auswahl von vier Kugeln zu ordnen?
$\Large {\frac{n!}{(n - k)!} = \frac{6!}{(6 - 4)!} = \frac{6!}{2!}\frac{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6}{1 \dot 2} = \frac{720}{2} = 360}$
Es gibt insgesamt also $360$ Möglichkeiten, vier Kugeln aus einer Menge von sechs Kugeln zu ziehen und diese in den unterschiedlichsten Kombinationen zu ordnen.
Variation mit Wiederholung
Merke
Um die Variation mit Wiederholung einer Auswahl von $k$ Objekten von einer Gesamtzahl an $n$ Objekten zu berechnen, benötigt man diese Formel:
$\Large{n^k}$
Beispiel
In einer Kiste befinden sich sechs verschiedenfarbige Kugeln, von denen vier Kugeln gezogen werden. Nach jedem Ziehen wird die gezogene Kugel zurück in die Urne gelegt. Wie viele mögliche Kombinationen an gezogenen Kugeln gibt es? Berechne die Kombinationen.
Anzahl $n$ aller Objekte: $6$
Anzahl $k$ der ausgewählten Objekte: $4$
$\Large{n^k = 6^4 = 1296}$
Es gibt insgesamt also $1296$ Möglichkeiten, vier Kugeln aus einer Menge von sechs Kugeln mit Zurücklegen zu ziehen und diese in den unterschiedlichsten Kombinationen zu ordnen.
Nun kennst du in der Kombinatorik alle Formeln und kannst die Permutation, Kombination und Variation berechnen. Teste dein neu erlerntes Wissen zum Thema Kombinatorik mit unseren Übungsaufgaben zur Kombinatorik!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Übungsaufgaben
In einer Kiste befinden sich vier verschiedenfarbige Kugeln, von denen zwei Kugeln gezogen werden. Nach dem Ziehen wird die gezogene Kugel wieder zurück in die Urne gelegt. Wie viele mögliche Kombinationen an gezogenen Kugeln gibt es?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Du möchtest mehr Aufgaben?
Teste kostenlos unser Lernportal mit vielen Übungen & Lösungen.
Du brauchst mehr Hilfe?
Wir unterstützen Dich!
Unsere Kunden über den Studienkreis
Feedback von Eltern & Schüler:innen
Weitere Erklärungen & Übungen zum Thema
Mathematik
> Wahrscheinlichkeitsrechnung und Statistik
Klassenstufen in Mathematik
Weitere Fächer
Lernen und Üben
Noch Fragen?
Wir sind durchgehend für dich erreichbar
