Vierfeldertafel erstellen - Beispielaufgabe mit Lösung
Die Vierfeldertafel ist ein wichtiges Instrument der Stochastik bzw. der Wahrscheinlichkeitsrechnung. Eine Vierfeldertafel hilft dir immer dann weiter, wenn du eine Aufgabe hast, bei der zwei verschiedene Ereignisse $A$ und $B$ betrachtet werden. Zu jedem dieser Ereignisse kannst du ein Gegenereignis formulieren, sodass du insgesamt vier Möglichkeiten erhältst:
- Ereignis A: $A$
- Gegenereignis von A: $ \overline {A}$
- Ereignis B: $B$
- Gegenereignis von B: $ \overline {B}$
Kombiniert man diese Ereignisse und Gegenereignisse, ergeben sich insgesamt vier Kombinationen:
- $A$ und $B$
- $A$ und $\overline {B}$
- $B$ und $\overline{A}$
- $\overline {B}$ und $\overline {A}$
Allgemeine Form einer Vierfeldertafel
Wir können die Kombinationsmöglichkeiten der Ereignisse in eine Tabelle schreiben, die aus vier Feldern besteht. In diese vier Felder werden die absoluten Häufigkeiten der vier Kombinationen eingetragen. Die Kombination aus zwei Ereignissen wird als Schnittmenge bezeichnet; die zwei Ereignisse werden mit dem mathematischen Zeichen für "und" ($\cap$) verbunden. Die Vierfeldertafel bildet die bedingte Wahrscheinlichkeit, also die Kombinationsmöglichkeiten von Ereignissen, ab.
Merke
Am Ende jeder Zeile bzw. Spalte stehen die absoluten Häufigkeiten der vier Ereignisse. Diese lassen sich durch Addition der Schnittmengen berechnen (siehe "Gesamt").
Im Feld unten rechts steht die Gesamtzahl. Diese entspricht der Summe aus den absoluten Häufigkeiten für die Ereignisse $A$ und $\overline {A}$ bzw. $B$ und $\overline {B}$.
Du kannst dir hier eine vorlage-vierfeldertafel herunterladen.
Eine Vierfeldertafel muss nicht aus absoluten Häufigkeiten bestehen. Es gibt drei unterschiedliche Darstellungsformen:
- Absolute Häufigkeit
- Relative Häufigkeit in Dezimalschreibweise
- Relative Häufigkeit in Prozent
Eine Alternative zur Vierfeldertafel ist das Baumdiagramm. Schau dir auch diese Möglichkeit an.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Bedingte Wahrscheinlichkeit mit Vierfeldertafel berechnen - Beispielaufgabe
Am besten versteht man die Vierfeldertafel anhand eines Beispiels.
Beispiel
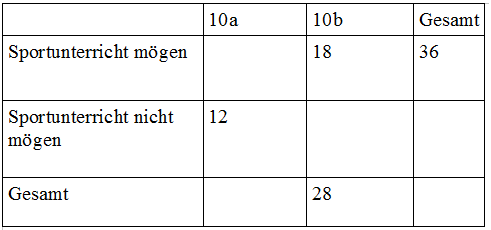
Wir untersuchen, wie viele Schüler der 10. Jahrgangsstufe den Mathematikunterricht mögen. Die Jahrgangsstufe besteht aus den zwei Klassen 10a und 10b.
Die Untersuchung ergab, dass 9 Schüler aus Klasse 10b den Mathematikunterricht mögen. Die Klasse 10b besteht aus 36 Schülern. In der Klasse 10a befinden sich 12 Schüler, die den Mathematikunterricht nicht mögen. Insgesamt mögen 27 Schüler der 10. Jahrgangsstufe den Mathematikunterricht.
Unsere erste Aufgabe ist es, die Ereignisse A und B zu erkennen.
- Ereignis $A$ ist in diesem Fall die Klasse 10a; das entsprechende Gegenereignis ist die Klasse 10b.
- Ereignis $B$ ist das Merkmal "den Mathematikunterricht mögen;" das Gegenereignis dementsprechend das Merkmal "den Mathematikunterricht nicht mögen."
Wenn wir die Ereignisse bestimmt haben, können wir die Vierfeldertafel erstellen.
Die Lücken füllen wir zunächst einmal mit Text aus, um zu verstehen, was die einzelnen Schnittmengen bedeuten:
Wir wissen jetzt, welche Zahl in welches Feld der Vierfeldertafel gehört.
Im nächsten Schritt tragen wir nun alle absoluten Häufigkeiten ein, die uns aus der Aufgabe bekannt sind:
- 9 Schüler aus der Klasse 10b mögen den Mathematikunterricht.
- Insgesamt besteht die Klasse 10b aus 36 Schülern.
- 12 Schüler aus der Klasse 10a mögen den Mathematikunterricht nicht.
- Insgesamt gibt es 27 Schüler in der 10. Jahrgangsstufe, die den Mathematikunterricht mögen.
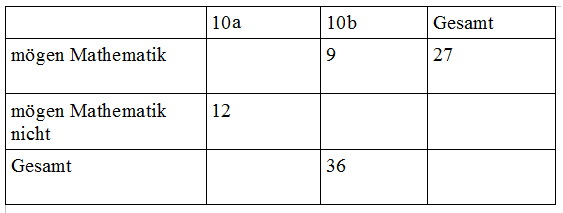ausgefüllte Vierfeldertafel
Wenn alle Zahlen eingetragen sind, die wir aus der Aufgabenstellung kennen, können wir die Zahlen, die in die leeren Felder gehören, berechnen. Wie du bereits weißt, stehen am Ende jeder Zeile bzw. Spalte die Gesamtzahlen, die du durch einfache Addition erhältst. Wenn du also in einer Zeile oder Spalte zwei Angaben gegeben hast, kannst du die dritte einfach ausrechnen. Also suchen wir in unserer Tabelle nach einer Zeile oder Spalte, die zwei Werte enthält.
In der ersten Zeile finden wir folgende Informationen:
- Insgesamt mögen 27 Schüler der 10. Jahrgangsstufe den Mathematikunterricht.
- Aus der Klasse 10b mögen 9 Schüler den Mathematikunterricht.
Wie viele Schüler aus der Klasse 10a mögen also den Mathematikunterricht? Wir ziehen einfach von der Gesamtzahl $27$ die $9$ Schüler der Klasse 10b ab und erhalten so die Anzahl der Schüler aus Klasse 10a, die den Mathematikunterricht mögen: $18$
Durch den errechneten Wert haben wir nun auch zwei Angaben in der ersten Spalte und können so nach und nach die Vierfeldertafel vervollständigen.
Wenn wir alle Werte errechnet haben, bleibt nur noch das Feld unten rechts übrig. In diesem Feld steht die Gesamtzahl aller Schüler, die sich aus der Addition sowohl der Zeile "Gesamt" als auch der Spalte "Gesamt" ergibt. Dieser letzte Schritt ist gleichzeitig eine gute Probe, um zu kontrollieren, ob wir richtig gerechnet haben. Stimmen die Summen nicht überein, haben wir einen Fehler beim Ausfüllen der leeren Felder gemacht.
In diesem Fall haben wir richtig gerechnet:
- 30 + 36 = 66
- 27 + 39 = 66
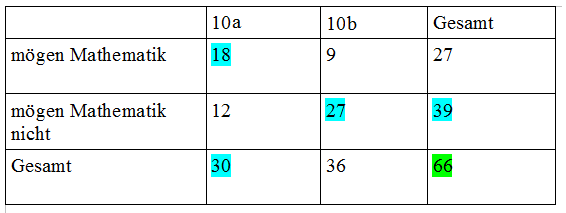Vierfeldertafel ausfüllen (3)
Methode
Darstellungsform der Werte in einer Vierfeldertafel
Wie du ja bereits gelernt hast, können wir in die Felder einer Vierfeldertafel entweder die absoluten Häufigkeiten schreiben oder die relativen Häufigkeiten oder die Prozentangaben.
Beim Umrechnen der absoluten Häufigkeiten in Prozentangaben setzt du das untere rechte Feld mit $ 100 \%$ gleich und errechnest die relativen Anteile der anderen Werte.
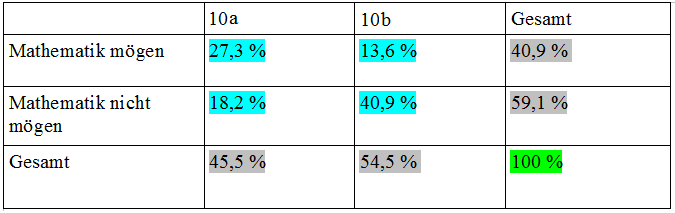
Beispiel
Wie groß ist der relative Anteil der Schüler, die die Klasse 10a besuchen und den Mathematikunterricht nicht mögen?
- absolute Häufigkeit: 12 Schüler
- relativer Anteil: $\frac{12}{66} \approx 0,1818 ~~\widehat{=}~~ 18,2 \%$
Wichtig: Oft erhältst du keine glatten Zahlen, sodass du deine Ergebnisse runden musst. Du musst dabei darauf achten, dass du deine Ergebnisse entweder alle auf eine Nachkommastelle oder alle auf zwei Nachkommastellen rundest und beim Runden keine Fehler machst.
Gut zu wissen
Nachdem wir nun eine Vierfeldertafel erstellt haben, können wir auch nach der Wahrscheinlichkeit für ein bestimmtes Ereignis fragen:
Wie groß ist die Wahrscheinlichkeit, dass ein zufällig ausgewählter Schüler der 10. Jahrgangsstufe aus der 10b kommt und den Mathematikunterricht mag?
Ereignis: $E=\{\overline{A} \cap B\}$ ("10b" und "Matheunterricht mögen")
Wahrscheinlichkeit: $P(E)=\frac{9}{66} \approx 0,1364 ~~\widehat{=}~~ 13,6 \%$
Die Wahrscheinlichkeit, dass ein zufällig ausgewählter Schüler der 10. Jahrgangsstufe die Klasse 10b besucht und den Mathematikunterricht mag, beträgt also ca. $13,6 \%$.
Regeln zum Erstellen einer Vierfeldertafel
Merke
(1) Ereignisse und Gegenereignisse erkennen und eine leere Vierfeldertafel zeichnen.
(2) Alle brauchbaren Angaben aus der Aufgabenstellung in die Vierfeldertafel eintragen.
(3) Fehlende Werte mit Hilfe der Zeilen-/Spaltensumme ausrechnen.
(4) Ergebnisse mit Hilfe der Zeilen- und Spaltensumme "Gesamt" überprüfen.
Teste dein neu erlerntes Wissen zum Thema Vierfeldertafel mit unseren Aufgaben und Übungen!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Welche Möglichkeiten der Darstellungsform hast du in einer Vierfeldertafel?
Was kannst du aus einer Vierfeldertafel ablesen?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
