Es ist wichtig, unter anderem auch für die Wahrscheinlichkeitsrechnung, dass du den Unterschied zwischen der absoluten und der relativen Häufigkeit kennst.
Du benötigst diese beiden Begriffe sehr oft beim Beschreiben von Wahrscheinlichkeitsexperimenten, aber auch im Umgang mit Prozentangaben.
Absolute Häufigkeit
Um den Unterschied zwischen absoluter und relativer Häufigkeit besser zu verstehen, erklären wir dies anhand eines Beispiels: Stell dir vor, du hast zwei unterschiedlich große Bonbontüten vor dir liegen. In beiden Tüten befinden sich gelbe, grüne und rote Bonbons. Dir schmecken vor allem die grünen Bonbons sehr gut und du möchtest wissen, wie viele grüne Bonbons jeweils in der großen und der kleinen Tüte sind. Um das herauszufinden, kannst du die grünen Bonbons einfach zählen.
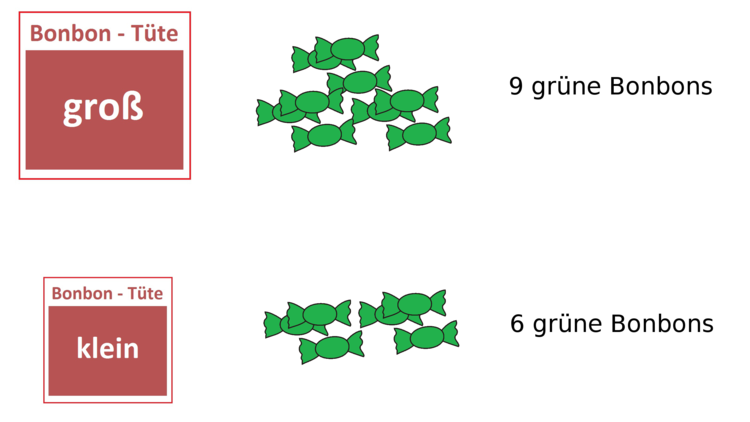
Wie du siehst, befinden sich in der großen Bonbontüte neun grüne Bonbons und in der kleinen Tüte nur sechs.
Ohne es vielleicht gemerkt zu haben, haben wir soeben die absolute Häufigkeit von grünen Bonbons in zwei unterschiedlich großen Tüten bestimmt. Die absolute Häufigkeit gibt also einfach die Anzahl von grünen Bonbons an. Du erhältst die absolute Häufigkeit durch einfaches Zählen - du musst nicht rechnen. Die absolute Häufigkeit wird in den meisten Fällen in ganzen Zahlen (auch absolute Zahlen genannt) angegeben.
Merke
Die absolute Häufigkeit beschreibt die Anzahl von Elementen oder Objekten mit einem bestimmten Merkmal. Sie wird durch Zählen ermittelt und in der Regel mit einer ganzen Zahl angegeben.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
Relative Häufigkeit
Der Unterschied der relativen zur absoluten Häufigkeit steckt schon im Namen: relativ bedeutet so viel wie "verhältnismäßig" oder "von bestimmten Bedingungen abhängig". Aber zu welcher Größe können wir die Häufigkeit in ein Verhältnis setzen?
Betrachten wir erneut unser Beispiel mit den grünen Bonbons. Wir haben bereits festgestellt, dass in der kleinen Tüte weniger Bonbons sind. Da wir zwei unterschiedlich große Bonbontüten untersucht haben, ist es für uns natürlich auch noch wichtig zu wissen, wie viele grüne Bonbons jeweils im Verhältnis zum Inhalt der ganzen Tüte enthalten sind. Um das herauszufinden, müssen wir zunächst die Gesamtzahl der Bonbons in den beiden Tüten ermitteln.
Wir kennen jetzt die Anzahl der grünen Bonbons (absolute Häufigkeit) und die Gesamtzahl der Bonbons pro Tüte. Nun können wir ohne Probleme die relative Häufigkeit der grünen Bonbons errechnen:
$relative\ Häufigkeit = \frac{absolute~Häufigkeit}{Gesamtanzahl}$
- große Tüte: $\frac{ \textcolor{green}{9}}{36} = 0,25 ~\widehat{=}~25 \%$
- kleine Tüte: $\frac{ \textcolor{green}{6}}{12} = 0,5 ~\widehat{=}~ 50 \%$
Merke
Die relative Häufigkeit setzt die absolute Anzahl eines Ereignisses in ein Verhältnis zum Ganzen. Sie wird in Prozent angegeben und hat somit in der Dezimalschreibweise einen Wert zwischen 0 und 1.
Die relative Häufigkeit ist also nichts anderes als das, was du vielleicht schon unter dem Begriff des relativen Anteils kennst. Wenn wir uns nun noch einmal unsere Ergebnisse angucken, erkennen wir, dass die absolute Häufigkeit der grünen Bonbons in der großen Tüte zwar größer ist, die relative Häufigkeit dort jedoch kleiner ist. Es lohnt sich also eher viele kleine Tüten zu kaufen als wenige große.
In den Übungsaufgaben kannst du jetzt dein Wissen testen. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen! Übungsaufgaben
140 von 800 Schülern einer Schule essen gerne Gemüse.
Welcher relativen Häufigkeit entspricht dies?
Du brauchst mehr Hilfe? Wir unterstützen Dich!
Bewertung bundesweit
Unsere Kunden über den Studienkreis Feedback von Eltern & Schüler:innen
Studienkreis Nachhilfe Deutschland:
4.60 / 5.00 Sterne bei 3700 Bewertungen
Weitere Erklärungen & Übungen zum Thema Mathematik > Wahrscheinlichkeitsrechnung und Statistik
Klassenstufen in Mathematik
Weitere Fächer Lernen und Üben
Noch Fragen? Wir sind durchgehend für dich erreichbar
