Stochastische Abhängigkeit und Unabhängigkeit
Die Wahrscheinlichkeit eines Ereignisses bei einem Zufallsexperiment kann von einem anderen Ereignis unabhängig oder abhängig sein. Schauen wir uns diese beiden Möglichkeiten im Folgenden etwas genauer an.
Unabhängige Ereignisse bei mehrstufigen Zufallsexperimenten
Wir ziehen zweimal hintereinander eine Kugel aus einer Urne mit vier grünen und sechs lila Kugeln. Nach jedem Zug legen wir die gezogene Kugel zurück in die Urne.
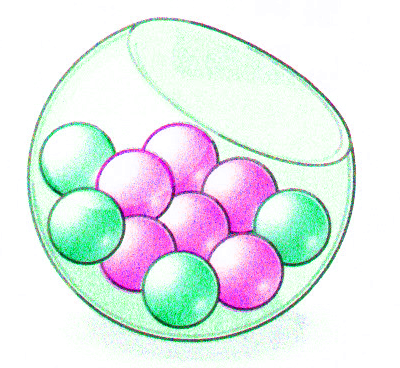
Die Wahrscheinlichkeiten, eine Kugel einer bestimmten Farbe zu ziehen, lassen sich leicht berechnen:
- $P (grün) = \frac{4}{10} = 0,4 ~~\widehat{=}~~40 \%$
- $P (lila) = \frac{6}{10} = 0,6 ~~\widehat{=}~~60 \%$
Da die gezogene Kugel nach dem ersten Zug wieder zurück in die Urne gelegt wird, ändern sich die Wahrscheinlichkeiten vor dem 2. Zug nicht.
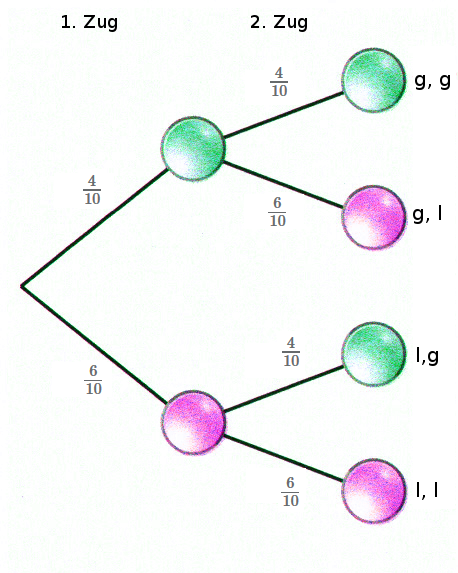
Bei Zufallsexperimenten mit dem Urnenmodell bleiben die Wahrscheinlichkeiten unverändert, wenn die Kugeln nach dem Ziehen wieder zurück in die Urne gelegt werden.
Merke
Zwei Ereignisse A und B heißen voneinander (stochastisch) unabhängig, wenn das Eintreten des einen Ereignisses die Wahrscheinlichkeit für das Eintreten des anderen Ereignisses nicht verändert.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Abhängige Ereignisse bei mehrstufigen Zufallsexperimenten
Wir betrachten nochmal unsere Urne mit den vier grünen und den sechs lila Kugeln. Auch dieses Mal ziehen wir zweimal hintereinander, aber: wir legen die Kugel nach dem ersten Zug nicht zurück in die Urne.
Die Wahrscheinlichkeiten vor dem ersten Zug sind dieselben wie oben:
1. Zug
- $P (grün) = \frac{4}{10} = 0,4 ~~\widehat{=}~~40 \%$
- $P (lila) = \frac{6}{10} = 0,6 ~~\widehat{=}~~60 \%$
Beim zweiten Zug ändern sich allerdings die Bedingungen: Wenn wir die erste Kugel nach dem ersten Zug nicht wieder zurück in die Urne legen, ändert sich die Anzahl der Kugeln in der Urne und somit auch der relative Anteil ( = $\frac{Anzahl~an~Kugeln~einer~bestimmten~Farbe}{Anzahl~aller~Kugeln}$).
Die Anzahl an grünen und lila Kugeln ändert sich in Abhängigkeit des Ergebnisses des ersten Zuges.
Beispiel
Wir ziehen im ersten Zug eine lila Kugel.
Vor dem zweiten Zug sind die Wahrscheinlichkeiten also wie folgt:
- $P (grün) = \frac{4}{9} \approx 0,4444 ~~\widehat{=}~~44,44 \%$
- $P (lila) = \frac{5}{9} \approx 0,5556 ~~\widehat{=}~~55,56 \%$
Die Wahrscheinlichkeiten vor dem 2. Zug hängen also von dem Ergebnis des 1. Zuges ab. Dementsprechend ändern sich auch die Wahrscheinlichkeiten an den Ästen des Baumdiagrammes.
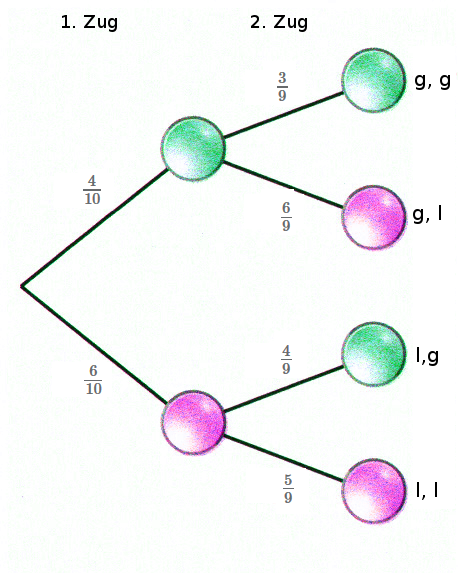
Merke
Zwei Ereignisse A und B heißen voneinander (stochastisch) abhängig, wenn das Eintreten des einen Ereignisses die Wahrscheinlichkeit für das Eintreten des anderen Ereignisses beeinflusst.
Bei Zufallsexperimenten mit stochastischer Abhängigkeit ändern sich die Wahrscheinlichkeiten nach jedem Durchgang.
Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben! Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
