Baumdiagramme erstellen und verstehen
Um beim Rechnen mit Wahrscheinlichkeiten einen guten Überblick zu behalten, legen wir sogenannte Baumdiagramme an. Aus einem Baumdiagramm kannst du die unterschiedlichen Ausgänge, und die jeweiligen Wahrscheinlichkeiten, eines Zufallsexperimentes ablesen. Der große Vorteil solcher Baumdiagramme ist, dass du auch mehrstufige Zufallsexperimente übersichtlich darstellen kannst.
Betrachten wir zwei Baumdiagramme für die Versuche "einmaliges bzw. zweimaliges Werfen einer Münze."
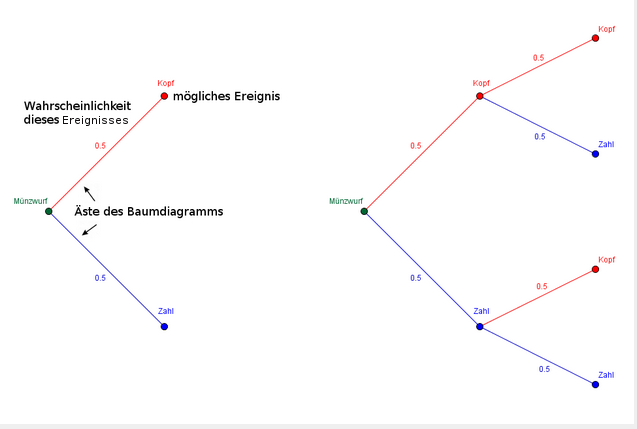
Wie du siehst, stehen am Ende der Linien (auch Äste genannt) die beiden möglichen Ereignisse (Kopf, Zahl). An den Ästen steht jeweils die zu dem Ereignis gehörende Wahrscheinlichkeit in der Dezimalschreibweise (in diesem Fall immer 0,5). Nachdem du die Münze einmal geworfen hast, besteht beim zweiten Wurf wieder eine jeweils 50%ige Wahrscheinlichkeit, dass Kopf oder Zahl oben liegt. Man schreibt diese zwei neuen Möglichkeiten jeweils an die beiden möglichen Ereignisse des ersten Wurfs.
Merke
Merke
Mit Hilfe eines Baumdiagramms kannst du ein- oder mehrstufige Zufallsexperimente übersichtlich darstellen.
Erstellen komplexer Baumdiagramme
Bei einem Münzwurf sind die Wahrscheinlichkeiten sehr einfach verteilt, sodass ein Baumdiagramm nicht unbedingt notwendig ist. Bei einer komplexeren Verteilung der Wahrscheinlichkeiten hilft uns das Baumdiagramm jedoch den Sachverhalt gut und übersichtlich darzustellen - und dank zwei kleiner Regeln können wir mit Hilfe des Baumdiagramms sogar rechnen.
Schauen wir uns dazu dieses Glücksrad an:
Der Pfeil kann nach dem Drehen des Rades entweder auf Rot, Grün oder Blau zeigen. Die Wahrscheinlichkeiten dieser drei Ereignisse sind jedoch nicht gleich groß. So ist es zum Beispiel am wahrscheinlichsten, dass der Pfeil auf einem grünen Feld stehen bleibt, denn es gibt mehr grüne Felder als rote bzw. blaue Felder.
Wie sieht das Baumdiagramm aus, wenn du das Glücksrad zweimal hintereinander drehst?
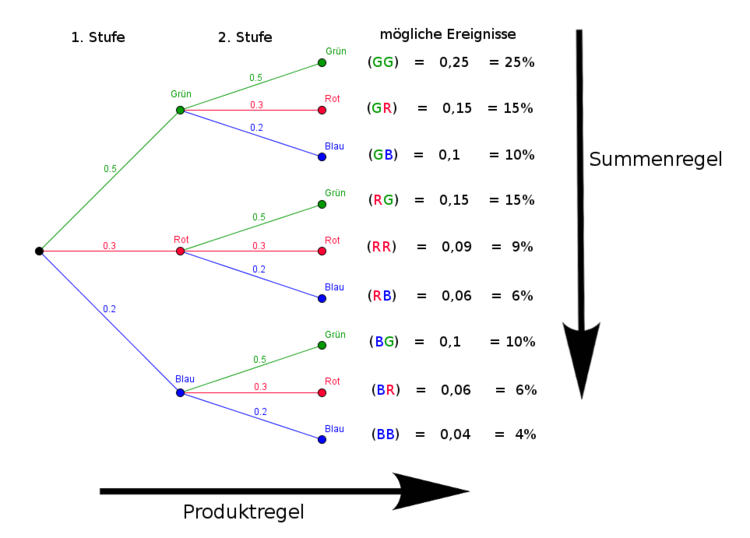
Die Wahrscheinlichkeiten für die Farben ergeben sich aus den relativen Anteilen:
- grün: fünf von zehn Feldern = $\frac {5}{10} = 0,5$
- rot: drei von zehn Feldern = $\frac{3}{10} = 0,3$
- blau: zwei von zehn Feldern = $\frac{2}{10} = 0,2$
Auf der rechten Seite, also am Ende des Baumdiagramms, stehen die Wahrscheinlichkeiten für die verschiedenen Kombinationsmöglichkeiten (Ereignisse), die sich beim zweimaligen Drehen des Glücksrades ergeben. Addieren wir alle Wahrscheinlichkeiten, erhalten wir 100 %. Außerdem ergeben alle Wahrscheinlichkeiten, die auf den Ästen einer Spalte stehen, zusammen immer eins. Doch wie kommt man überhaupt auf diese Wahrscheinlichkeiten?
Merke
Merke
Mehrstufige Zufallsexperimente lassen sich sehr übersichtlich mit Hilfe eines Baumdiagramms darstellen. Alle möglichen Ergebnisse werden mit jeweils einem Pfad im Baumdiagramm dargestellt. Bei einem vollständigen Baumdiagramm kannst du die Kontrolle machen: Die Summe der Wahrscheinlichkeiten in einer Spalte muss immer 1 ergeben.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Die Produktregel
Betrachten wir als Beispiel die Wahrscheinlichkeit für das Ereignis, dass das Glücksrad im ersten Versuch bei Grün und im zweiten Versuch bei Blau stehen bleibt. Es handelt sich hier um ein Elementarereignis, also um ein Ereignis, das aus nur einem Ergebnis besteht. Wir gucken uns nun lediglich den Teil des Baumdiagramms an, der dieses Ereignis beschreibt. Den Weg, den man verfolgen muss um ein Ereignis zu beschreiben, nennt man Pfad.
Um die Wahrscheinlichkeit des Ereignisses "grünes Feld, blaues Feld" zu berechnen, musst du die Wahrscheinlichkeiten entlang des Pfades multiplizieren.
$P (\textcolor{green}{G} \textcolor{blue}{B}) = P(\textcolor{green}{G}) \cdot P(\textcolor{blue}{B})$
$P (\textcolor{green}{G} \textcolor{blue}{B}) = \textcolor{green}{0,5} \cdot \textcolor{blue}{0,2} = 0,1~~\widehat{=}~~10 \%$
Die Wahrscheinlichkeit, dass das Glücksrad nach dem ersten Drehen auf einem grünen Feld und nach dem zweiten Drehen auf einem blauen Feld stoppt, beträgt 10 %.
Die Wahrscheinlichkeiten aller anderen Kombinationsmöglichkeiten (Ereignisse) lassen sich analog berechnen. Probiere es selber aus! Du kannst deine Lösungen dann mit den Wahrscheinlichkeiten in der Grafik oben vergleichen.
Merke
Merke
Produktregel
Bei einem mehrstufigen Zufallsversuch berechnest du die Wahrscheinlichkeit eines Ereignisses, indem du die Wahrscheinlichkeiten entlang des Pfades, der zu dem Ereignis führt, miteinander multiplizierst.
Die Summenregel
Mit Hilfe des Baumdiagramms kannst du aber nicht nur die Wahrscheinlichkeit eines Ereignisses (bzw. Elementarereignisses) berechnen, sondern auch die Wahrscheinlichkeit eines Ereignisses, das aus mehreren Ergebnissen besteht.
Betrachten wir das Ereignis "mindestens einmal das rote Feld treffen." Zu diesem Ereignis gehören mehrere Ergebnisse:
$E = \{ \textcolor{green}{G} \textcolor{red}{R}, \textcolor{red}{R} \textcolor{green}{G}, \textcolor{red}{RR}, \textcolor{red}{R} \textcolor{blue}{B}, \textcolor{blue}{B} \textcolor{red}{R}\}$
Um die Wahrscheinlichkeit für diese Ereignismenge zu berechnen, musst du die Wahrscheinlichkeiten der einzelnen Ereignisse addieren:
$P (E) = P(\textcolor{green}{G} \textcolor{red}{R}) + P (\textcolor{red}{R} \textcolor{green}{G}) + P (\textcolor{red}{RR}) + P(\textcolor{red}{R} \textcolor{blue}{B}) + P (\textcolor{blue}{B} \textcolor{red}{R})$
Die Wahrscheinlichkeiten aller möglichen Ereignisse hast du oben schon mithilfe der Produktregel berechnet:
$P (E) = 0,15 + 0,15 + 0,09 + 0,06 + 0,06 = 0,51 ~~\widehat{=}~~51 \%$
Die Wahrscheinlichkeit für das Ereignis, dass der Pfeil, bei zweimaligem Drehen, mindestens einmal auf einem roten Feld stoppt, beträgt $51\%$.
Merke
Merke
Summenregel
Die Wahrscheinlichkeit eines Ereignisses, das aus mehreren Ergebnissen besteht, berechnest du, indem du die Wahrscheinlichkeiten der einzelnen Ereignisse addierst.
Mit den Übungsaufgaben kannst du nun überprüfen, ob du alles richtig verstanden hast. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Welche Wahrscheinlichkeit muss auf dem Ast stehen?
Welche Regeln musst du beim Arbeiten mit dem Baumdiagramm beachten?
Wie lautet die Wahrscheinlichkeit für das Ereignis $P(\textcolor{blue}{Blau} \textcolor{red}{Rot}$ oder $\textcolor{red}{Rot} \textcolor{red}{Rot})$?
(in Dezimalschreibweise)
Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, musst du die Wahrscheinlichkeiten entlang des Pfades ... .
Wie muss der Satz enden? Kreuze an!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Weitere Erklärungen & Übungen zum Thema
Hol dir Hilfe beim Studienkreis und frag einen Lehrer!
Du benötigst Hilfe bei einer Aufgabe? Nutze die Mathematik-Hausaufgabenhilfe und bespreche deine Aufgabe sofort ohne Termin per Online-Chat mit einem Mathematik-Lehrer.
- Sofort, ohne Termin
- Online-Chat 14 – 21 Uhr
- Erfahrene Mathematik-Lehrer
Du benötigst häufiger Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik Online-Nachhilfe und verbessere deine Mathematik-Kenntnisse.
- Zum Wunschtermin
- Online-Einzelgespräch
- Geprüfte Nachhilfelehrer
Du möchtest lieber einen Lehrer der Mathematik-Nachhilfe aus deiner Stadt im persönlichen und direkten Gespräch fragen? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Zum Wunschtermin
- In deiner Stadt
- Geprüfte Nachhilfelehrer
- Nachhilfe Berlin
- Nachhilfe München
- Nachhilfe Nürnberg
- Nachhilfe Köln
- Nachhilfe Düsseldorf
- Nachhilfe Dortmund
- Nachhilfe Hamburg
- Nachhilfe Hannover
- Nachhilfe Bremen
- Nachhilfe Leipzig
- Nachhilfe Dresden
Standort nicht gefunden? Rund 1000 Nachhilfe-Standorte bundesweit!
Nachhilfe gesucht
Du möchtest mehr Aufgaben? Zugriff auf alle Aufgaben erhältst du im Studienkreis Lernportal.
- Über 250.000 Übungsaufgaben
- 700 Lernvideos
- Original-Abi-Klausuren
Unsere Kunden über den Studienkreis
Wir sind durchgehend für dich erreichbar
(kostenlos und jederzeit)
