In diesem Kapitel befassen wir uns mit dem Kreisdiagramm. Es wird hauptsächlich in der Prozentrechnung verwendet, um Größen im Vergleich besser darstellen zu können. Beispiele aus dem Alltag sind vor allem Wahlergebnisse oder auch Statistiken aus der Wirtschaft.
Aufbau eines Kreisdiagrammes
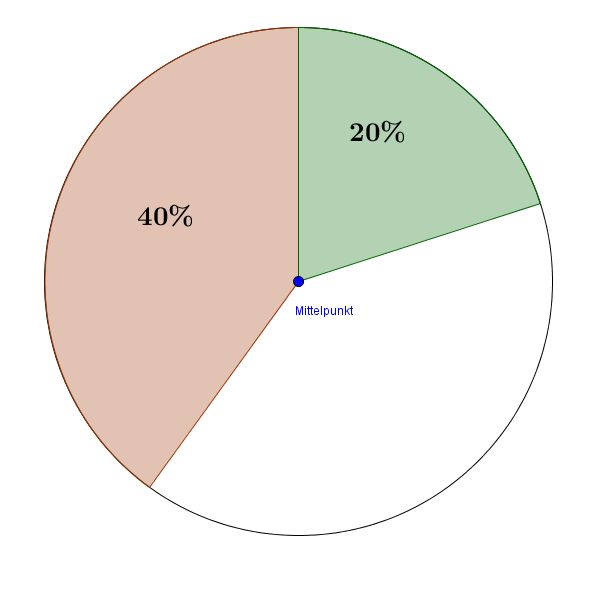
Um ein Kreisdiagramm zu erstellen zeichnest du als erstes einen Kreis. Dieser Kreis in seiner Gesamtheit bildet genau 100%. Wenn du jetzt einen Anteil einzeichnen möchtest, in unserer Abbildung $40\%$ und $20\%$, dann musst du den Anteil von $360°$ errechnen. Also:
$Winkel \; = \; 360° \cdot \large{ \frac{\textcolor{blue}{40\%}}{100\%}}$
$\Leftrightarrow Winkel \; = \; 360° \cdot 0,40$
$\Leftrightarrow Winkel \; = \; 144° $
Die Zahl in $\textcolor{blue}{blau}$ ist der Winkel, der eingetragen werden muss. Er ist somit variabel. Allgemein sieht die Formel also wie folgt aus:
Merke
Der Winkel für einen Anteil in einem Kreisdiagramm lässt sich durch folgende Formel errechnen:
$Winkel \; = \; 360° \cdot \large{ \frac{\textcolor{blue}{x\%}}{100\%}}$
In der folgenden Abbildung haben wir die Prozentzahlen $20 \%$ und $40 \%$ eingetragen. Dazu haben wir die obige Formel genutzt, um den dazugehörigen Winkel, $72°$ und $144°$ herauszubekommen.
Um diesen Winkel dann in das Diagramm einzutragen, legst du das Geodreieck an den Kreis an und zeichnest die Winkel nebeneinander ein, so wie in der Abbildung.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
Beispiel eines Kreisdiagramms
Beispiel
Am letzten Sonntag waren Wahlen in der Stadt Bergstedt. Dabei waren $4$ Parteien beteiligt und konnten gewählt werden. Eindeutiger Sieger war die Partei FFK mit $60 \%$ der Wählerstimmen. Die Parteien BML und MLB haben jeweils mit $5 \%$ knapp den Einzug in den Stadtrat geschafft. Die restlichen Stimmen hat die Partei "Freiheit" erhalten.
a.) Wie viel Prozent der Stimmen hat die Partei "Freiheit" bekommen?
b.) Zeichne ein Kreisdiagramm zum Wahlausgang.
Um die erste Teilaufgabe lösen zu können, musst du die einzelnen Prozentzahlen zusammenrechnen und diese von $100\%$ abziehen. Es ergibt sich:
$x = 100 \% - 60 \% - 5 \% - 5 \% \Leftrightarrow x = 30 \%$
Die Lösung ist also $30 \%$.
Die zweite Teilaufgabe setzt einen Kreis voraus. Diesen zeichnen wir als erstes ein und benutzen dann die Formel zur Berechnung des Winkels.
Wir gehen also die einzelnen Winkel durch und erhalten:
$Winkel \; = \; 360° \cdot \large{ \frac{\textcolor{blue}{60\%}}{100\%}} \Leftrightarrow Winkel \; = 216°$
$Winkel \; = \; 360° \cdot \large{ \frac{\textcolor{blue}{5\%}}{100\%}}\Leftrightarrow Winkel \; = 18°$
$Winkel \; = \; 360° \cdot \large{ \frac{\textcolor{blue}{30\%}}{100\%}}\Leftrightarrow Winkel \; = 108°$
Zeichnen wir die Winkel nun in das Kreisdiagramm ein, ergibt sich folgendes Kreisdiagramm:
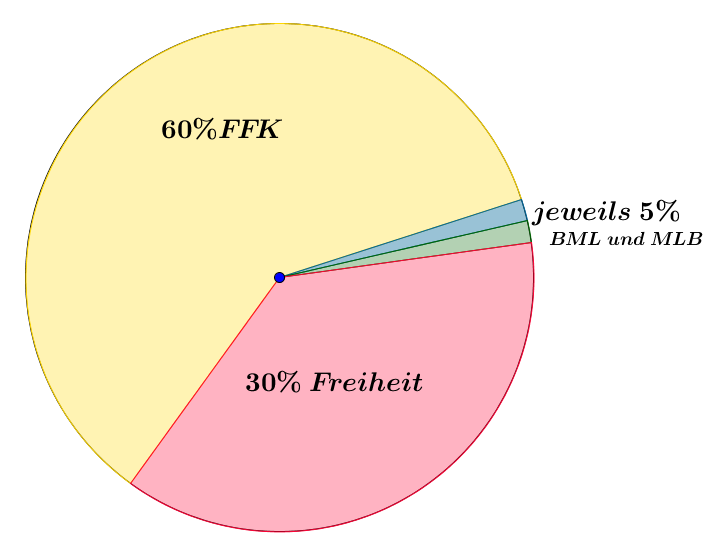
Beim Zeichnen des Kreisdiagramms, benötigst du nicht unbedingt Farben, um die einzelnen Parteien kenntlich zu machen. Es ist jedoch ratsam, zumindest die Bedeutung der einzelnen Teilbereiche aufzuschreiben, damit du weißt, welcher Kreisbogen zu welcher Partei gehört.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Übungsaufgaben
Du möchtest mehr Aufgaben?
Teste kostenlos unser Lernportal mit vielen Übungen & Lösungen.
Du brauchst mehr Hilfe?
Wir unterstützen Dich!
Unsere Kunden über den Studienkreis
Feedback von Eltern & Schüler:innen
Weitere Erklärungen & Übungen zum Thema
Mathematik
> Wahrscheinlichkeitsrechnung und Statistik
Klassenstufen in Mathematik
Weitere Fächer
Lernen und Üben
Noch Fragen?
Wir sind durchgehend für dich erreichbar
