Zufallsversuche - Wahrscheinlichkeit von Ergebnissen berechnen
Eines der bekanntesten Wahrscheinlichkeitsexperimente ist der Zufallsversuch. Zufällig sind hierbei die Ergebnisse des Versuchs. In diesem Lerntext werden wir dir das Thema Zufallsversuche erklären und zu diesem Teil der Wahrscheinlichkeitsrechnung Aufgaben mit dir durchgehen. So wirst du dieses Thema schnell verstehen und keine Probleme mehr mit dem Rechnen mit Zufallsversuchen haben.
Wahrscheinlichkeiten von Zufallsversuchen berechnen
Die Berechnung der Wahrscheinlichkeiten der möglichen Ergebnisse folgt einer einfachen Regel.
Merke
Bei einfachen Zufallsexperimenten gilt:
Wahrscheinlichkeit = $\frac {Anzahl\ der\ gewünschten\ Ergebnisse}{Anzahl\ aller\ möglichen\ Ergebnisse}$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Zufallsexperimente - Aufgaben
Wahrscheinlichkeit: Aufgabe 1
Ein typisches Beispiel für einen solchen Zufallsversuch ist das Werfen einer Münze. Wenn eine Münze geworfen wird, sind die möglichen Ergebnisse Kopf oder Zahl. Die jeweilige Wahrscheinlichkeit, dass eines dieser Ergebnisse eintritt, liegt in beiden Fällen bei $50 \%$. Theoretisch ist es auch denkbar, dass die Münze auf der schmalen Kante landet. Dieses extrem unwahrscheinliche Ereignis bleibt in den folgenden Beispielen zur Wahrscheinlichkeitsrechnung ungeachtet.
Wahrscheinlichkeit = $\frac {Anzahl\ der\ gewünschten\ Ergebnisse}{Anzahl\ aller\ möglichen\ Ergebnisse} = \frac{1}{2} = 0,5 $
Wahrscheinlichkeit: Aufgabe 2
Auch das Werfen eines Würfels ist ein klassischer Zufallsversuch. Ein normaler sechsseitiger Würfel besitzt für jede Seite dieselbe Wahrscheinlichkeit:
Wahrscheinlichkeit = $\frac {Anzahl\ der\ gewünschten\ Ergebnisse}{Anzahl\ aller\ möglichen\ Ergebnisse} = \frac{1}{6} = 0,1667 = 16,67\%$
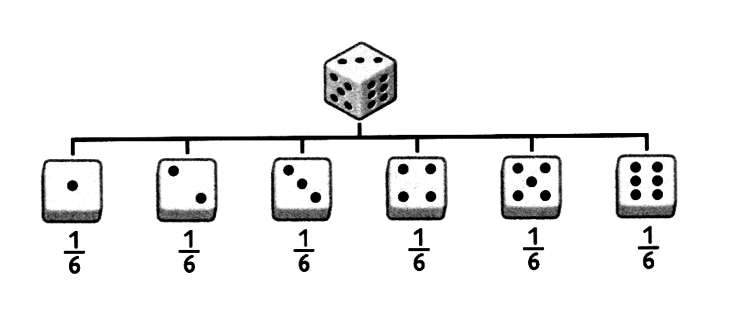
Laplace-Versuche
Merke
Das Werfen einer Münze oder eines Würfels sind sogenannte Laplace-Versuche. Ein Laplace-Versuch ist ein Zufallsexperiment, dessen mögliche Ergebnisse alle gleich wahrscheinlich sind.
Zufallsversuche mit ungleichen Wahrscheinlichkeiten
Auch wenn es auf den ersten Blick etwas ungewöhnlich wirkt, gibt es auch Zufallsversuche, deren mögliche Ergebnisse nicht gleich wahrscheinlich sind.
Ein Beispiel wäre ein Würfel, der nicht sechs unterschiedliche Seiten besitzt, wie in diesem Beispiel:
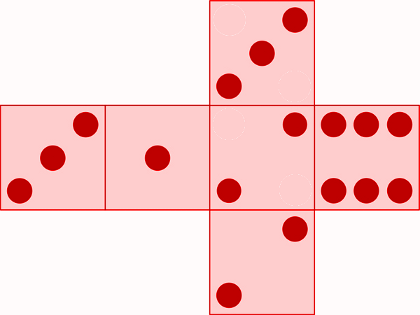
Wie du siehst, sind nicht alle Zahlen auf diesem Würfel vertreten: die $3$ und die $2$ befinden sich je auf zwei Seiten, wohingegen die $4$ und die $5$ gar nicht vorkommen.
Im Gegensatz zum normalen Würfel sind die Wahrscheinlichkeiten für jedes der möglichen Ergebnisse ($1, 2, 3, 6$) unterschiedlich.
- $P(1) = \frac {1}{6} = 0,1667 = 16,67\%$
- $P(2) = \frac {2}{6} = 0,3333 = 33,33\%$
- $P(3) = \frac {2}{6} = 0,3333 = 33,33\%$
- $P(4) = \frac {0}{6} = 0 = 0\%$
- $P(5) = \frac {0}{6} = 0 = 0\%$
- $P(6) = \frac {1}{6} = 0,1667 = 16,67\%$
Teste dein neu erlerntes Wissen zur Wahrscheinlichkeitsverteilung mit unseren Aufgaben!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema