Was ist ein Winkel und welche Winkelarten gibt es?
Im folgenden Lerntext geben wir dir einen Einblick in die Geometrie. Hierbei wird der Winkel betrachtet, was er ist, wie er entstehen kann, welche besonderen Winkel es gibt und wie du ihn mithilfe des Geodreiecks berechnen kannst.
Was ist ein Winkel?
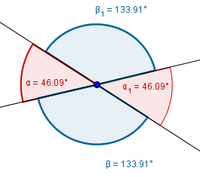
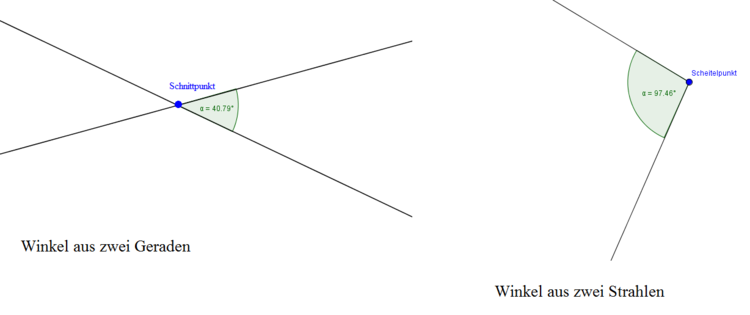
Wenn sich zwei Geraden schneiden, entstehen Winkel. An dem Schnittpunkt der beiden Geraden befinden sich vier Winkel, wovon je zwei, die gegenüberliegenden, die gleiche Größe haben. Es kann auch sein, dass ein Winkel durch zwei Strahlen entsteht. Der gemeinsame Anfangspunkt der beiden Strahlen ist dann der Scheitelpunkt des Winkels.
Im Alltag begegnen uns Winkel überall: Dächer haben einen Neigungswinkel, jede Tür steht mit einem bestimmten Winkel offen, Flugzeuge heben von der Startbahn mit einem bestimmten Winkel ab, Straßen haben Steigungswinkel, geometrische Figuren haben Winkel und es gibt noch viele weitere Beispiele.
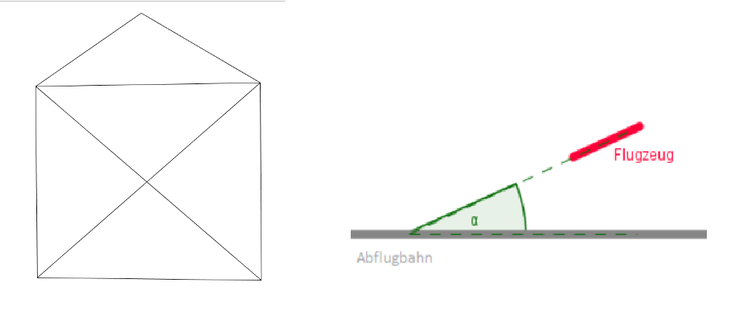
Ein Flugzeug, welches abhebt oder auch landet hat immer einen Winkel zur Landebahn. Auch das Haus vom Nikolaus, welches eine geometrische Figur ist, hat viele verschiedene Winkel.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Winkelgrößen
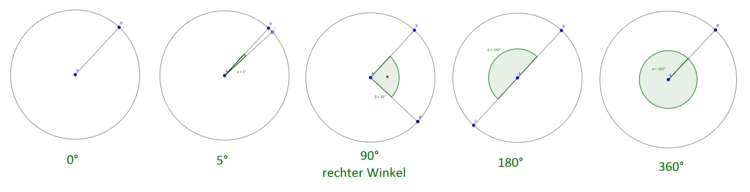
Winkel werden in Grad ($^\circ$) angegeben. Die Gradzahlen sind zwischen $0^\circ$ und $360^\circ$ groß.
Bei $0^\circ$ existiert kein Winkel, bei $5^\circ$ ist er ganz klein. Ein rechter Winkel entsteht, wenn der Winkel $90^\circ$ beträgt, bei $180^\circ$ erhalten wir eine Gerade und bei $360^\circ$ einen Kreis.
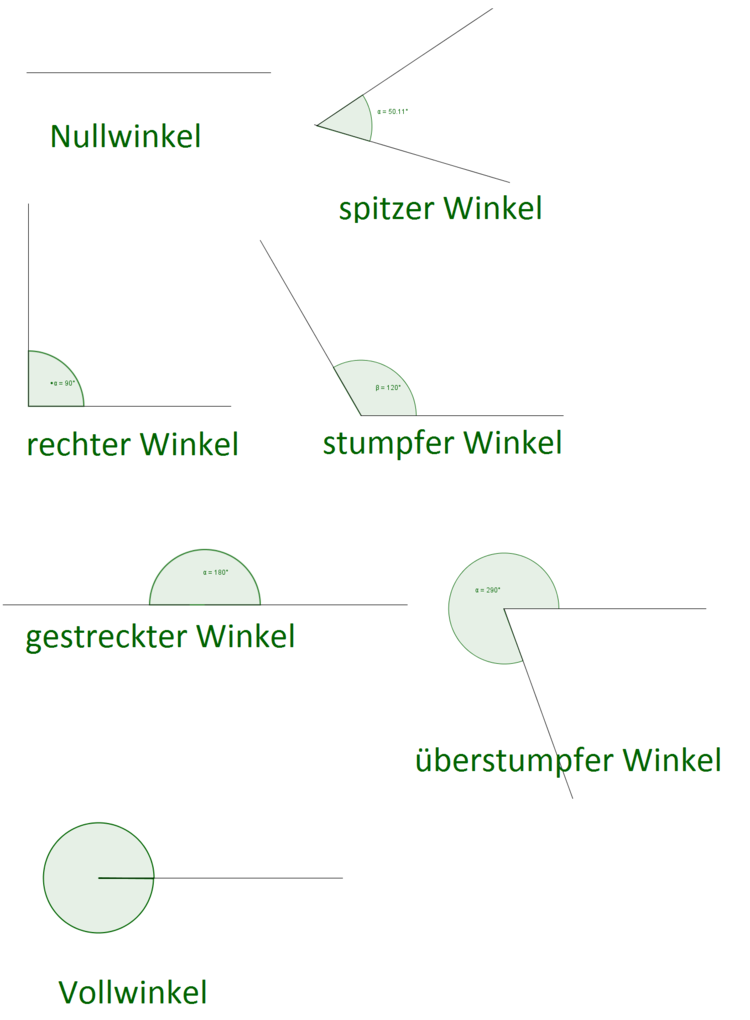
Winkelarten
Es gibt verschiedene Winkelarten. Je nach Gradzahl besitzen manche Winkel eine bestimmte Bezeichnung. So heißt ein Winkel, der $90^\circ$ groß ist, rechter Winkel. Oder eine Gerade, die eine Winkelgröße von $180^\circ$ hat, gestreckter Winkel.
Außerdem gibt es noch Namen für Winkel, die zwischen zwei festgelegten Gradzahlen liegen, wie zum Beispiel spitze Winkel, die größer als $0^\circ$ und kleiner als $90^\circ$ sind.
Winkel mit dem Geodreieck messen
Die Größe eines Winkels kann mit einem Geodreieck gemessen werden.
Methode
Vorgehensweise
- Das Geodreieck muss mit der Nullstelle auf dem Schnittpunkt des Winkels liegen.
- Die Kante des Geodreiecks muss nun an einer Geraden anliegen. Dabei soll das Geodreieck auf dem Winkel liegen.
- Nun muss die richtige Winkelskala ausgesucht werden. Die Winkelskala, die auf dem Geodreieck an der Geraden anliegt und bei null startet, ist die Richtige.
- Nun muss der Wert abgelesen werden. Notiere dir den abgelesenen Wert und überprüfe, ob der Winkel größer oder kleiner als ein rechter Winkel ist. Dann vergleiche mit dem zu messenden Winkel.
Selbstverständlich haben wir auch Beispiele und Übungsaufgaben zum Thema Winkel mit dem Geodreieck messen.
Winkel zeichnen
Wir können mit Hilfe des Geodreiecks auch Winkel einer bestimmten Größe zeichnen. Dafür gehen wir wie folgt vor:
Methode
Vorgehensweise
- Eine Gerade zeichnen.
- Das Geodreieck an die Gerade so anlegen, dass der Nullpunkt am Ende der Geraden liegt.
- Den angegebenen Winkel ablesen und mit einem Punkt markieren.
- Den Endpunkt der Gerade mit dem Markierungspunkt verbinden.
Du kannst dir auch unsere Beispiele und Übungsaufgaben zum Thema Winkel mit dem Geodreieck zeichnen anschauen. Dein erlerntes Wissen über den Winkel und die verschiedenen Winkelarten kannst du in unseren Übungen festigen. Wir wünschen dir dabei viel Spaß!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema