Kreis und Dreieck mithilfe eines Zirkels zeichnen
Der Zirkel ist ein praktisches Werkzeug der Geometrie. Mit ihm können nicht nur Kreise gezeichnet werden, sondern er ist auch ein Hilfsmittel für viele weitere Konstruktionen. Du hast sicher schon mal einen Zirkel gesehen:

Kreis zeichnen
Die Metallspitze des Zirkels wird vorsichtig in das Blatt gedrückt. Dann wird der Zirkel an der oberen Spitze angepackt und einmal gedreht. Schon erhalten wir einen Kreis. Mit dem Zirkel können Kreise eines bestimmten Radius bzw. Durchmessers gezeichnet werden.
Dafür geht man wie folgt vor:
Radius - Kreis zeichnen
Man nehme ein Lineal oder Geodreieck und setze die Spitze des Zirkels an den Punkt null. Dann verstellt man den Zirkel so, dass die zweite Spitze bis zur Zahl reicht, dessen Größe der Radius haben soll. Schauen wir uns dies einmal anhand eines Beispiels an:
Beispiel
Der Radius des zu zeichnenden Kreises soll $2,5 cm$ betragen.
Als erstes stellen wir den Zirkel so ein, dass die Spitze den Nullpunkt des Geodreiecks berührt und die Bleistiftspitze die $2,5 cm$ Markierung:

Als zweites zeichnen wir dann den Kreis:

Der Kreis mit dem Radius $2,5 cm$ ist fertig gezeichnet.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Durchmesser - Kreis zeichnen
Wenn der Durchmesser gegeben ist, muss der Wert durch zwei geteilt werden:
Merke
$Radius= \frac{Durchmesser}{2}$
Denn dann erhalten wir den Radius und können wie oben vorgehen.
Beispiel
Wir sollen einen Kreis mit einem Durchmesser von $10 cm$ zeichnen. Versuche deinen Zirkel richtig einzustellen und zeichne danach den Kreis.
Zunächst muss der Zirkel eingestellt werden. Der Durchmesser soll $10 cm$ betragen, also muss der Abstand zwischen den beiden Zirkelspitzen, der gleich dem Radius ist, $5cm$ betragen. Nun muss nur noch der Kreis gezeichnet werden.
Anwendungsaufgabe - Dreieck konstruieren
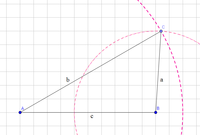
Wenn wir drei Seitenlängen eines Dreiecks gegeben haben und dieses konstruieren sollen, benötigen wir als Hilfsmaterial einen Zirkel. Um ein Dreieck mit drei bestimmten Seitenlängen zu konstruieren gehen wir wie folgt vor:
Methode
Vorgehensweise:
- Eine der drei gegebenen Seitenlängen einzeichnen.
- Die Länge einer zweiten Seite mit dem Zirkel abmessen und einen Kreisausschnitt um einen der Punkte zeichnen.
- Die dritte Länge mit dem Zirkel einstellen und um den anderen Punkt einen Kreisausschnitt zeichnen.
- Die beiden Kreisausschnitte treffen sich in einem Punkt. Diesen Punkt markieren wir.
- Nun den neuen Punkt mit den beiden Endpunkten der ersten Strecke verbinden.
Schauen wir uns ein Beispiel dazu an:
Beispiel
Konstruiere folgendes Dreieck:
$a= 6cm, b=3cm, c=5cm$
Wir zeichnen eine Seite. Nennen wir die Punkte $A$ und $B$, so muss die Seite $c$ bezeichnet werden, da sie später dem Punkt $C$ gegenüberliegt.

Nun zeichnen wir mit dem Zirkel erst den einen Kreis mit dem gegebenen Radius um den Punkt und danach den zweiten Kreis. Den Schnittpunkt der beiden Kreise markieren wir.
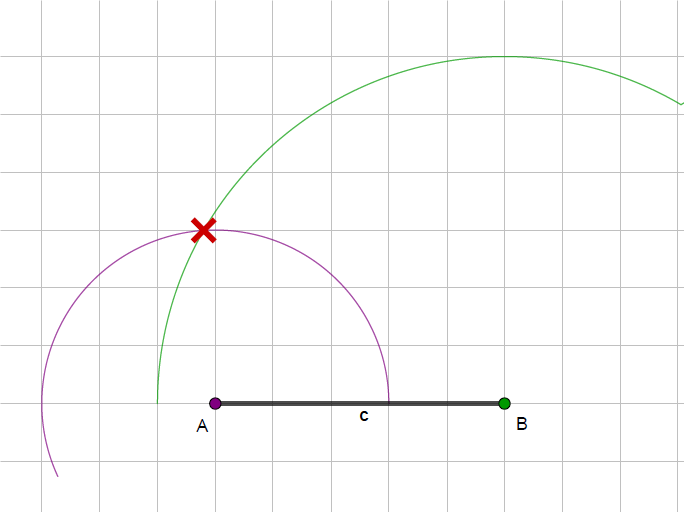
Nun müssen noch die Punkte verbunden werden und schon ist das Dreieck fertig konstruiert.

Nun hast du gelernt, wie du mit dem Zirkel einen Kreis mit einem bestimmten Radius oder Durchmesser zeichnen kannst. Außerdem haben wir uns eine Anwendungsaufgabe angeschaut. Vertiefe dein Wissen in den Übungsaufgaben. Viel Erfolg dabei!
Video: Simon Wirth
Text: Chantal Rölle
Teste dein Wissen!
Wie gehst du vor, wenn du einen Kreis mit einem bestimmten Radius zeichnen möchtest?
Wie groß musst du einen Zirkel einstellen, wenn du einen Kreis mit einem Durchmesser von $6 cm$ zeichnen möchtest?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema