Peripheriewinkelsatz und Umfangswinkelsatz - Erklärung und Beweis
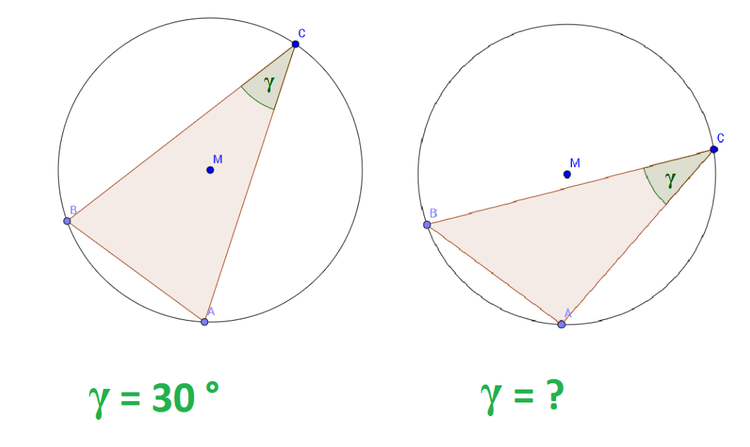
Der Umfangswinkelsatz, oder auch Peripheriewinkelsatz genannt, ist ein Satz in der Geometrie. Es handelt sich um ein Dreieck in einem Kreis, welches durch eine feste Sehne, hier die Strecke $\overline{AB}$ und einen beweglichen Punkt $C$ definiert ist. Dabei besagt der Umfangswinkelsatz, dass der Winkel am Punkt $C$ immer gleich groß ist.
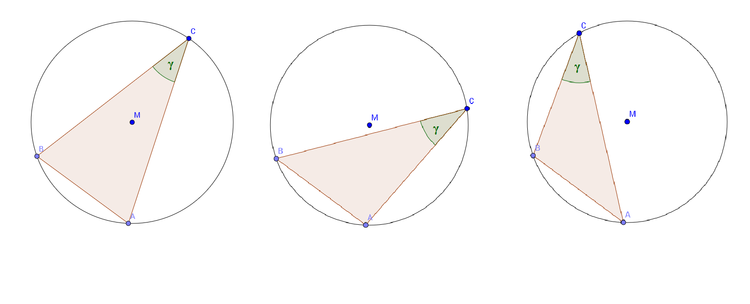
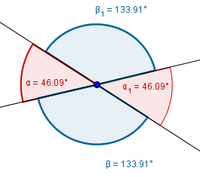
Wir sehen an der oberen Abbildung die Strecke $\overline{AB}$, die eine feste Sehne im Kreis ist. Der Punkt $C$ wurde nun auf der Kreislinie bewegt. Der Winkel an dem Punkt (hier $\gamma$) verändert sich nicht, seine Größe ist immer gleich.
Was sagt der Umfangwinkelsatz aus?
Merke
Der Umfangswinkelsatz besagt, dass der Umfangswinkel zur selben Kreissehne gleich groß ist.
Dieser Tatbestand kann bewiesen werden. Schauen wir uns den Beweis einmal an:
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beweis des Umfangwinkelsatz
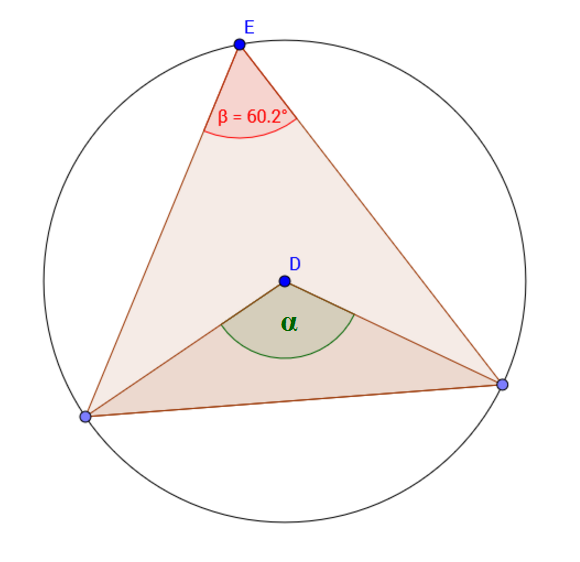
Um den Umfangswinkelsatz zu beweisen, müssen wir zunächst beweisen, dass der Mittelpunktswinkel doppelt so groß ist wie der Umfangswinkel. Die folgende Abbildung veranschaulicht dies:
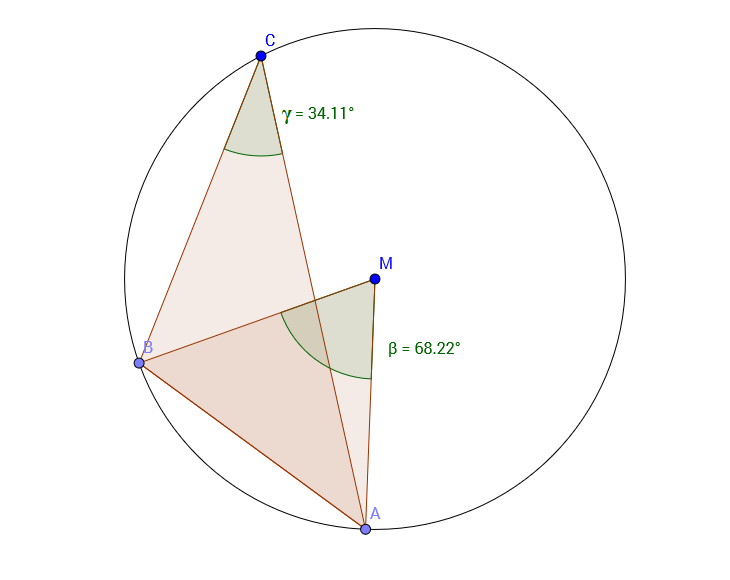
Wir sehen, dass der Mittelpunktswinkel $\beta = 68,22^\circ$ doppelt so groß ist, wie der Umfangswinkel $\alpha = 34,11^\circ$. Dies gilt es zu beweisen! Denn wenn wir dies bewiesen haben, haben wir auch den Umfangswinkelsatz bewiesen. Der Winkel am Mittelpunkt verändert sich beim Bewegen vom Punkt $C$ nicht. Dennoch bleibt der Winkel im Punkt C halb so groß wie der Winkel am Mittelpunkt.
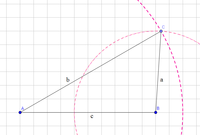
Wir ziehen vom Mittelpunkt zum Punkt $C$ eine Gerade und erhalten drei Dreiecke mit mehreren Winkeln:
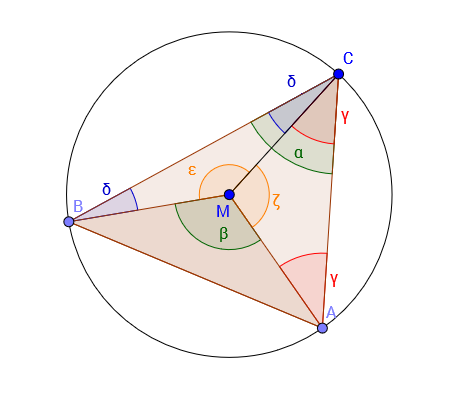
Wir wissen, dass die Innenwinkelsumme jedes beliebigen Dreiecks $180^\circ$ groß ist. Unser Ziel ist es zu beweisen, dass $\beta = 2\alpha$.
Starten wir mit der Bestimmung von $\delta $ und $\zeta$:
$180^\circ= \epsilon + 2\cdot \delta$
$\epsilon = 180^\circ -2 \delta$
$\zeta = 180^\circ -2 \gamma$
Wir wissen, dass in einem Kreis die Winkelsumme insgesamt aus $360^\circ$ beträgt. Dies wenden wir an:
$360^\circ = \epsilon + \zeta + \beta$
$\beta= 360^\circ -\epsilon - \zeta$
Setzen wir nun die zuvor bestimmten Terme für $\delta $ und $\zeta$ ein:
$\beta= 360^\circ - (180^\circ -2 \delta) - (180^\circ -2 \gamma)$
$\beta= 360^\circ - 180^\circ + 2\delta -180^\circ + 2 \gamma)$
$\beta = 2\delta + 2\gamma$
$\beta = 2 (\delta + \gamma)$
$\beta = 2 \alpha$
Damit ist bewiesen, dass der Umfangswinkel immer halb so groß ist wie der Mittelwinkel. Daraus können wir schließen, dass der Umfangswinkel immer gleich groß ist, da sich der Mittelpunktswinkel beim Bewegen von Punkt $C$ nicht verändert.
Mit den Übungsaufgaben kannst du dein neues Wissen jetzt testen. Viel Erfolg dabei!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema