Punktspiegelung - Schritt für Schritt erklärt
In diesem Text wird erklärt, wie eine Figur an einem Punkt gespiegelt wird.
Punktspiegelung
Bei der Punktspiegelung wird eine Figur um einen Spiegelpunkt gedreht. Schauen wir uns dies in der nachfolgenden Abbildung einmal an:
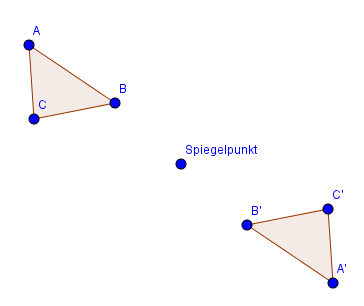
Die neu entstandenen Punkte werden Bildpunkte genannt und mit einem Apostroph versehen.
Wir sehen, dass das Dreieck $A'B'C'$ mit dem ursprünglichen Dreieck $ABC$ deckungsgleich ist. Dies bedeutet, dass wir das Dreieck $A'B'C'$ so verschieben und drehen können, dass es genau auf das Dreiecke $ABC$ passt. In der nachfolgenden Abbildung ist dies dargestellt:
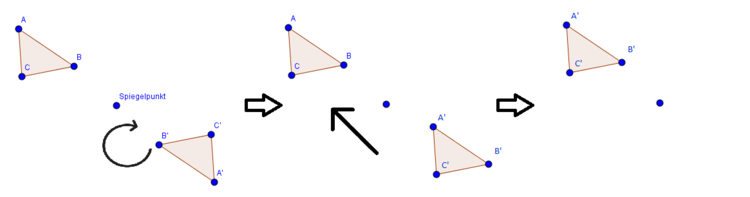
Schauen wir uns nun an, wie wir eine Figur an einem Punkt spiegeln können:
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Vorgehensweise
1. Mit dem Geodreieck
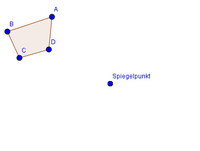
Wir haben den Spiegelpunkt und das Viereck gegeben.
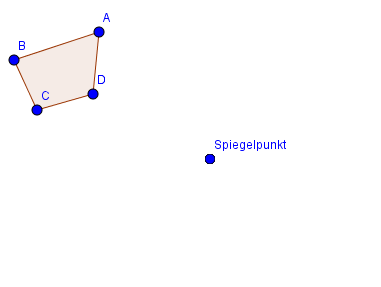
Die Punkte des Vierecks werden zunächst separat gespiegelt und dann werden die Bildpunkte zur Bildfigur verbunden. Um die Punktspiegelung durchführen zu können, benötigst du ein Lineal oder ein Geodreieck.
Lege das Geodreieck mit dem Nullpunkt auf den Spiegelpunkt und drehe es so, dass es einen Punkt des Vierecks berührt.
Nun wird abgelesen, wie weit der Punkt vom Spiegelpunkt entfernt ist. Der gleiche Abstand muss auf der anderen Seite des Spiegelpunktes markiert werden. Benenne anschließend den Bildpunkt deines Punktes, damit du später nicht durcheinanderkommst.
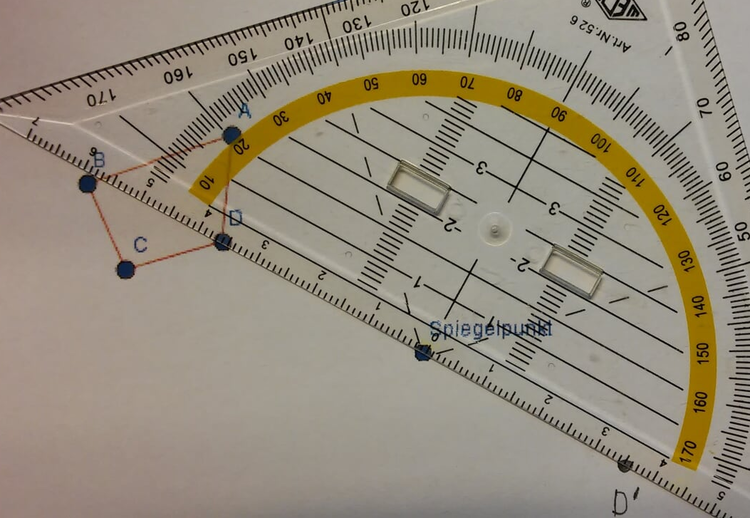
Alle anderen Punkte musst du auf die gleiche Weise spiegeln. Am Ende werden die gespiegelten Punkte in alphabetischer Reihenfolge verbunden.
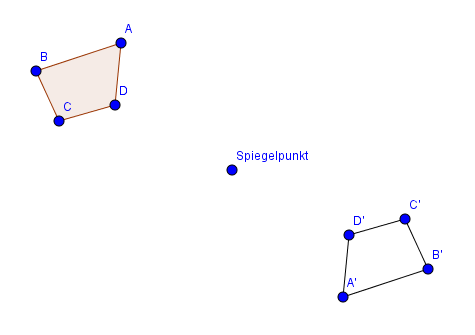
Die Vorgehensweise zusammengefasst:
Methode
- Das Geodreieck mit dem Nullpunkt auf den Spiegelpunkt legen und so verschieben, dass es den zu spiegelnden Punkt berührt.
- Den Abstand zwischen dem Punkt und dem Spiegelpunkt ablesen und auf der anderen Seite markieren.
- Den neu markierten Punkt - Bildpunkt - benennen. Er wird mit dem gleichen Buchstaben und einem Apostroph gekennzeichnet.
2. Mit dem Zirkel und einem Lineal
Wenn wir kein Geodreieck benutzen dürfen, ist die Punktspiegelung ein bisschen aufwendiger. Schauen wir uns dies an einem Beispiel an:
Beispiel
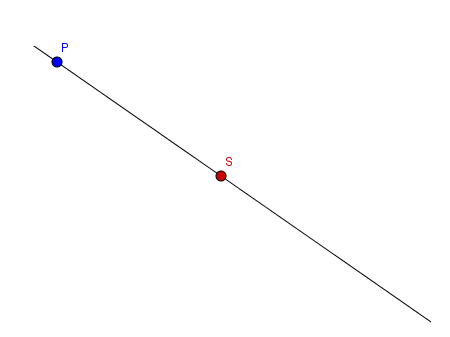
Der Punkt $P$ ist gegeben und soll mit Zirkel und Lineal am Spiegelpunkt $S$ gespiegelt werden. Das Lineal dient nur dazu, gerade Linien zeichnen zu können und darf nicht als Längenmessgerät verwendet werden. Denn sonst könnten wir wie oben beschrieben vorgehen.

Vorgehensweise
Methode
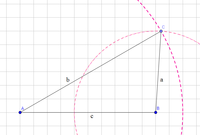
- Eine lange Gerade durch den Punkte $P$ und den Spiegelpunkt $S$ zeichnen.
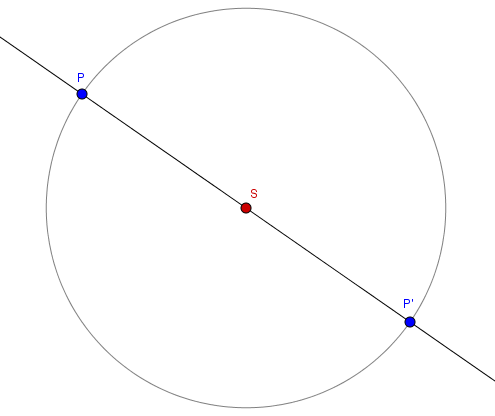
- Einen Kreis um den Spiegelpunkt zeichnen. Der Radius ist die Länge des Abstandes zwischen Punkt $P$ und dem Spiegelpunkt $S$.
- Der Kreis schneidet die zuvor gezeichnete Gerade in zwei Punkten: Ein Schnittpunkt ist der Punkt $P$ und der andere Schnittpunkt ist der Bildpunkt $P'$.
Mit den Übungsaufgaben kannst du dein Wissen zur Punktspiegelung überprüfen. Viel Erfolg dabei!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema