Winkel berechnen - Formel und Aufgaben
In diesem Lerntext erklären wir dir, mit welchen Tricks du Winkel berechnen kannst. Dazu werden wir in einem Dreieck Winkel berechnen und auch ein einem Viereck.
Winkelberechnung: Innenwinkelsumme berechnen
Die Innenwinkelsumme beschreibt, wie groß alle Winkel innerhalb einer geometrischen Figur zusammengerechnet sind.
So beträgt zum Beispiel die Innenwinkelsumme eines Dreiecks immer $180^\circ$ und die eines Vierecks $360^\circ$. Diese Erkenntnis kann uns helfen, wenn wir fehlende Winkel ausrechnen wollen.
Gut zu wissen
Man benötigt zwei Winkelangaben in einem Dreieck und drei Winkelangaben in einem Viereck, um jeweils den fehlenden Winkel zu berechnen.
Innenwinkelsumme Dreieck
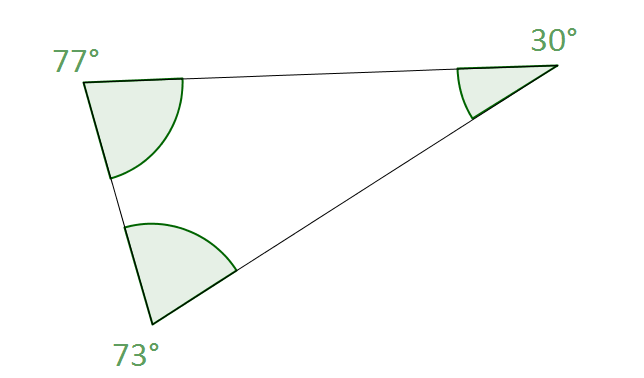
Wir können alle Winkel in diesem Dreieck zusammenrechnen und erhalten: $73^\circ+77^\circ+30^\circ = 180^\circ$. Das war auch schon die "Formel" mit der du Winkel im Dreieck zusammenrechnest.
Merke
In jedem Dreieck ergeben die Winkel zusammen immer $180^\circ$.
Innenwinkelsumme Viereck
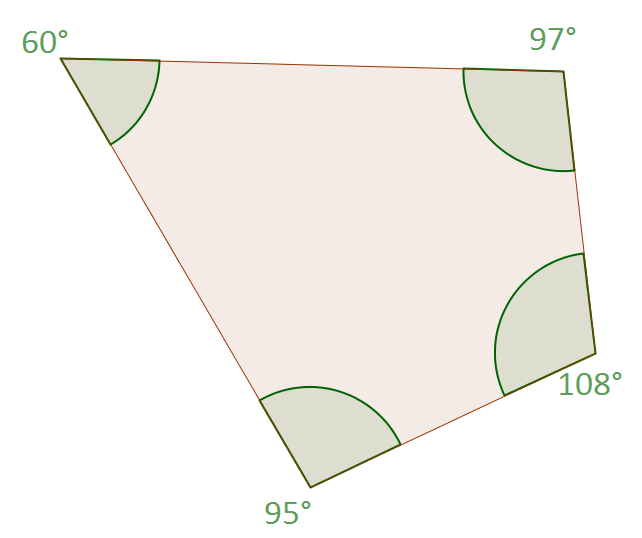
Wir können auch hier alle Winkel dieses Vierecks zusammenrechnen. $95^\circ+108^\circ+97^\circ+60^\circ = 360^\circ$. Wir sehen, dass alle Winkel zusammen $360^\circ$ ergeben. Dieses Ergebnis würden wir bei jedem beliebigen Viereck erhalten.
Merke
In jedem Viereck ergeben die Winkel zusammen immer $360^\circ$.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispielaufgabe: Berechnen eines Winkels mit Hilfe der Innenwinkelsumme
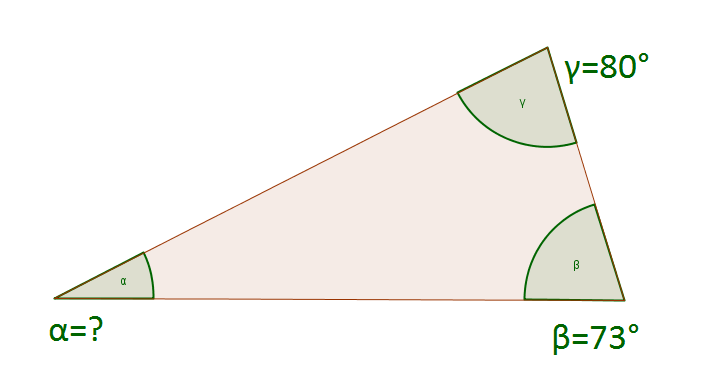
Wir haben dieses Dreieck gegeben und sollen den fehlenden Winkel $\alpha$ berechnen. Wir wissen, dass alle Winkel zusammen $180^\circ$ groß sein müssen. Wenn wir nun die beiden angegebenen Winkel von $180^\circ$ abziehen, erhalten wir die Größe des gesuchten Winkels $\alpha$.
$180^\circ = \alpha +\beta +\gamma$
$180^\circ =\alpha+ 73^\circ+80^\circ$ $|-73^\circ -80^\circ$
$\alpha = 180^\circ -73^\circ -80^\circ = 27^\circ $
Der Winkel $\alpha$ ist $27^\circ$ groß.
Formeln zu Sinus, Kosinus und Tangens
Die Größe eines Winkels in einem rechtwinkligen Dreieck kann mit den Winkelfunktionen Sinus, Kosinus und Tangens berechnet werden. Dabei sind nicht die anderen Winkelgrößen angegeben, sondern die Längen der Seiten des Dreiecks.
Um die Winkelfunktionen anwenden zu können, müssen wir zunächst die Seiten eines Dreiecks benennen können. Die Seiten eines Dreiecks werden auch Kathete genannt und jede Seite hat eine spezielle Bezeichnung:
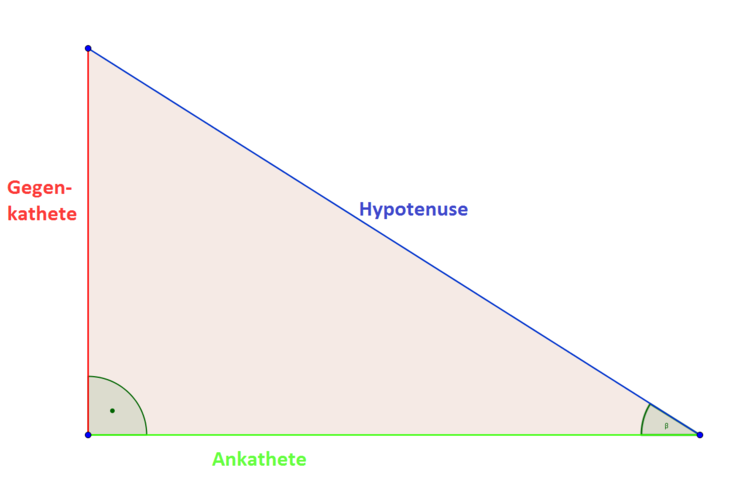
Die Hypotenuse ist immer die längste Seite eines rechtwinkligen Dreiecks. Sie liegt gegenüber von dem größten Winkel des rechtwinkligen Dreiecks, dem rechten Winkel. Die Gegen- und Ankathete beziehen sich beide auf einen der beiden spitzen Winkel. Hier ist dieser $\beta$. Die Gegenkathete ist gegenüber von dem gegebenen Winkel (hier $\beta$) und die Ankathete liegt direkt an dem Winkel dran (hier $\beta$).
Wenn nun zwei Seitenlängen gegeben sind können wir mit Sinus, Kosinus oder Tangens die dazugehörige Winkelgröße berechnen. Schauen wir uns hier die drei Formeln an:
Merke
$Sinus (\alpha) = \frac{Gegenkathete}{Hypotenuse}$
$Kosinus (\alpha) = \frac{Ankathete}{Hypotenuse}$
$Tangens (\alpha) = \frac{Gegenkathete}{Ankathete}$
Winkelberechnung mit Sinus, Kosinus und Tangens
Methode
- Benenne die Katheten.
- Was ist gesucht und was ist gegeben? Markiere dir dies in einer kleinen Skizze.
- Mit Hilfe der Skizze musst du nun überlegen, mit welcher Winkelfunktion du arbeiten kannst.
- Als letztes musst du nur noch die Angaben ausrechnen.
Schauen wir uns eine Beispielaufgabe zur Berechnung eines Winkels im Dreieck an:
Beispiel
Winkel
Um die Größe des Winkels α zu berechnen, musst du zuerst das Verhältnis von Gegenkathete zu Hypotenuse bestimmen. Also wird die Gegenkathete durch die Hypotenuse geteilt und das Ergebnis wird in die Umkehrfunktion von Sinus, also in $\sin^{−1}$, eingesetzt.
Beispiel
$\alpha=~?$, Hypotenuse $=6cm$, Gegenkathete $=3cm$
$\sin(\alpha)=\frac{Gegenkathete}{Hypotenuse}$
$\sin(\alpha)=\frac{3cm}{6cm}=0,5$
$\alpha=\sin^{−1}(0,5)=30^\circ$
Damit beträgt der Winkel $\alpha$ in dem Dreieck $30 ^\circ $.
Du weißt jetzt, wie du Winkel mithilfe der Sinus-, Kosinus- und Tangensfunktionen berechnen kannst. Du hast auch gelernt, dass es eine Innenwinkelsumme von Dreiecken und Vierecken gibt. Dein neu erlerntes Wissen kannst du nun in unseren Übungsaufgaben zu Winkeln und Winkelsummen im Dreieck und Viereck überprüfen. Viel Erfolg dabei!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema