Winkel messen mit einem Geodreieck
Das Geodreieck ist ein Hilfsmittel in der Geometrie. Es ist zum Messen und Zeichnen von Längen und Winkeln geeignet. In diesem Lerntext zeigen wir dir, wie du das Geodreieck verwenden musst, um die Größe eines Winkels zu messen.
Das Geodreieck

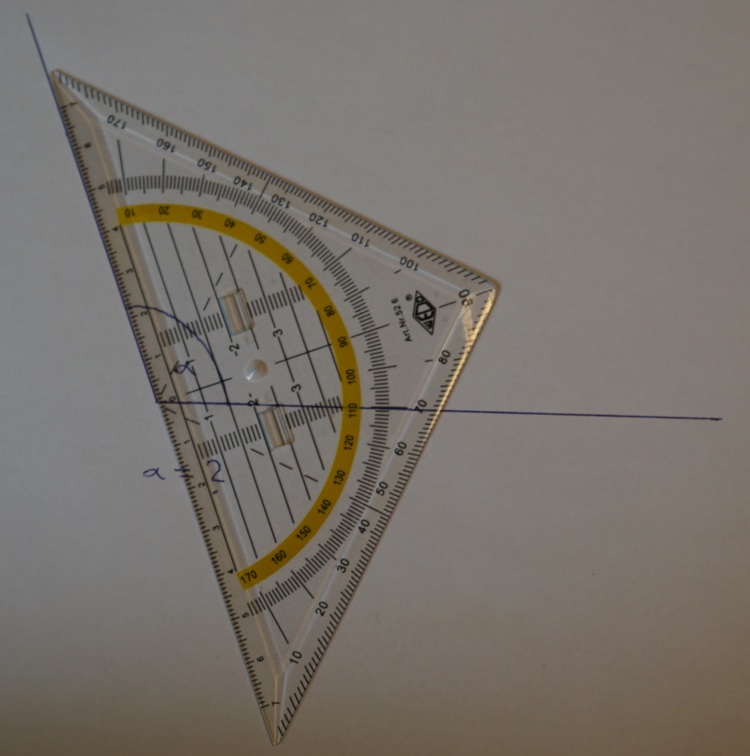
Die obige Abbildung zeigt dir ein Geodreieck. Mit Hilfe des Geodreiecks kannst du die Größe eines gezeichneten Winkels messen. Die Vorgehensweise wird im Folgenden beschrieben:
Winkel messen - Vorgehensweise
Methode
- Das Geodreieck muss mit dem Nullpunkt auf dem Scheitelpunkt des Winkels liegen.
- Die eine Hälfte der langen Seite des Geodreiecks muss außerdem auf einer der beiden Halbgeraden liegen.
- Nun muss die richtige Winkelskala ausgewählt werden. Die Winkelskala, die an der Halbgeraden mit null beginnt, ist die richtige.
- Jetzt kannst du die Größe des Winkels ablesen. Überprüfe dein Ergebnis, indem du die Zeichnung mit der Gradzahl vergleichst: Ist der gezeichnete Winkel kleiner oder größer als ein rechter Winkel und ist die abgelesene Gradzahl kleiner oder größer als $90^\circ$ - passen Zeichnung und Winkelgröße zusammen?
Anlegen des Geodreiecks
Beim Anlegen des Geodreiecks musst du ein wenig aufpassen. Wenn das Dreieck einmal richtig anliegt, können nur noch wenige Fehler auftreten.
Das Geodreieck muss mit dem Nullpunkt auf den Scheitelpunkt des Winkels gelegt werden. Nun muss das Geodreieck so gedreht werden, dass es mit der einen Hälfte seiner längsten Seite auf einer der beiden Halbgeraden liegt. Dabei muss darauf geachtet werden, dass der Nullpunkt auf dem Scheitel des Winkels bleibt.

Das Geodreieck kann auch am anderen Schenkel des Winkels angelegt werden.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Winkelskala auswählen
Es gibt zwei Winkelskalen. Nur jeweils eine Skala ist beim Ablesen des Winkels richtig. Diese beginnt an der Kante des Geodreiecks, die auf der Halbgeraden liegt, bei null. Wenn du den Winkel abgelesen hast, überprüfe noch einmal, ob du die richtige Skala gewählt hast. Du guckst dir den gezeichneten Winkel an und bestimmst, ob er kleiner oder größer als ein rechter Winkel ($90^\circ$) ist und vergleichst dann mit deinem abgelesenen Wert.

Auf dieser Abbildung ist die gelb unterlegte Skala die richtige. Sie beginnt an der Halbgeraden bei null.
Gegenwinkel messen
Mit dem Geodreieck können durch einfaches Anlegen nur Winkel gemessen werden, die kleiner als $180^\circ$ sind. Wenn der Winkel größer ist, müssen wir einen Trick anwenden: Wir messen zuerst den anderen Winkel (Gegenwinkel). Die Größe dieses Winkels wird dann von $360^\circ$ abgezogen. Schauen wir uns hierzu ein Beispiel an:
Beispiel
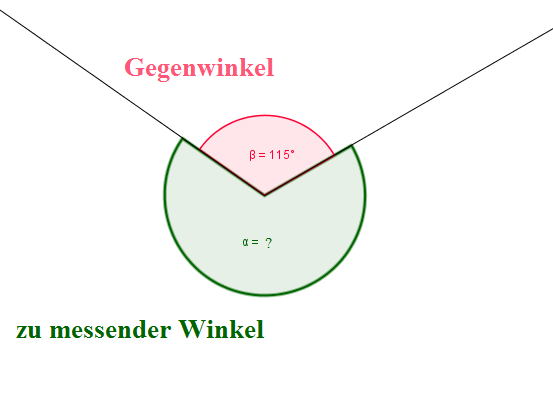
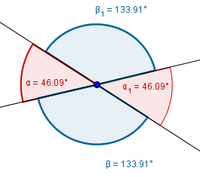
In der Abbildung erkennen wir, dass der Gegenwinkel von $\alpha$ der Winkel $\beta$ ist. $\beta$ ist $115 ^\circ$ groß. Also können wir berechnen: $ \alpha = 360 ^\circ - 115^\circ = 245^\circ$
Beispielaufgabe: Winkelgröße mit einem Geodreieck messen
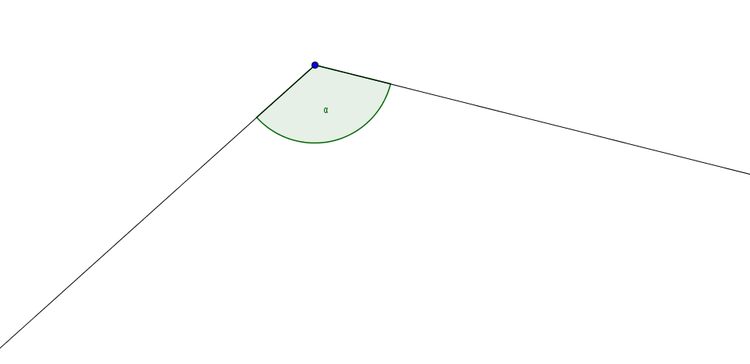
Der Winkel $\alpha$ soll bestimmt werden.
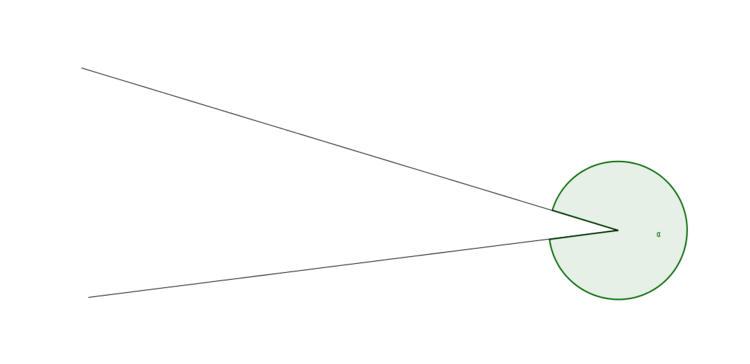
Druck dir das Bild aus und versuche die Größe des Winkels $\alpha$ mit dem Geodreieck zu messen.
Vertiefung
Lösung
Wir können den Winkel $\alpha$ nicht durch anlegen bestimmen, sondern müssen zunächst den Gegenwinkel messen und diesen dann von $360^\circ$ subtrahieren.
Das Geodreieck wurde mit dem Nullpunkt an den Scheitelpunkt so angelegt, dass du die Größe des Winkels einfach ablesen kannst.
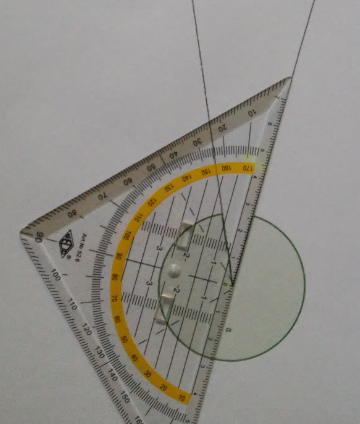
Wir können ablesen, dass der Winkel ca. $24^\circ$ beträgt.
$360^\circ-24^\circ = 336^\circ$

Der Winkel $\alpha$ beträgt also ungefähr $336^\circ$.
Wir haben nun alles besprochen, was du über das Winkelmessen wissen solltest. Mit den Übungsaufgaben kannst du testen, wie gut du das Thema verstanden hast! Dabei wünschen wir dir viel Spaß und Erfolg!
Teste dein Wissen!
Wie messen wir einen Winkel? Kreuze die richtige Reihenfolge an.
1. Notiere dir den abgelesenen Wert. Bestimme nun optisch, ob der Winkel kleiner oder größer als ein rechter Winkel ist. Überprüfe nun, ob dein gemessener Wert zu dem Winkel passen kann.
2. Die Kante des Geodreiecks muss außerdem auf der Halbgeraden liegen.
3. Das Geodreieck muss mit dem Nullpunkt auf dem Scheitelpunkt des Winkels liegen.
4. Nun muss die richtige Winkelskala ausgewählt werden. Die Winkelskala, die an der Halbgeraden mit null beginnt, ist die richtige.
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema