Spiegelpunkt und Spiegelachse konstruieren
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Den Spiegelpunkt finden
Ein Punkt $P$ und dessen Bildpunkt $P'$ sind gegeben. Wir sollen nun den Punkt bestimmen, an dem der Punkt $P$ gespiegelt wurde.
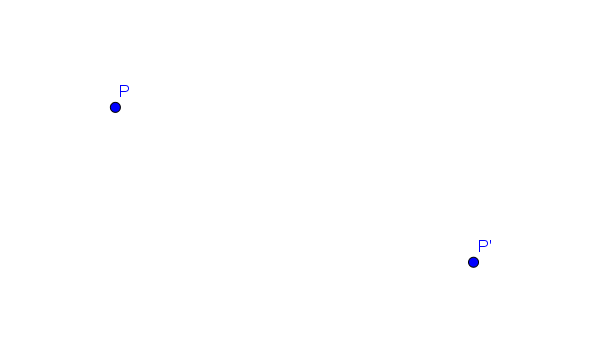
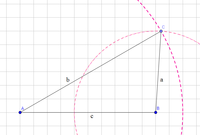
Um den Spiegelpunkt zu bestimmen, müssen wir je einen Kreis um die beiden Punkte zeichnen. Der Radius der beiden Kreise muss sowohl gleich groß sein als auch so groß, dass sich die beiden Kreise schneiden.
Da, wo sich die beiden Kreise schneiden, entstehen zwei Schnittpunkte (hier $A$ und $B$). Durch diese beiden Schnittpunkte ziehen wir eine Gerade.
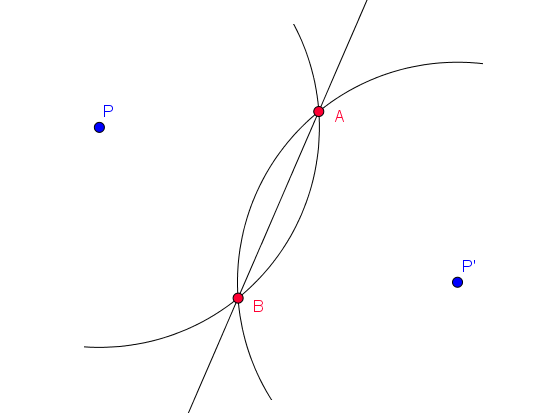
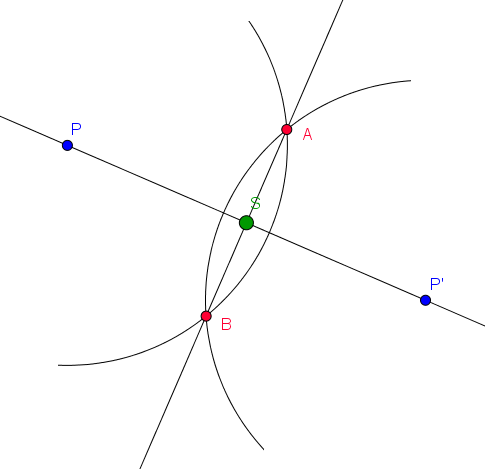
Jetzt wird noch eine Gerade durch die Punkte $P$ und $P'$ gezogen. Wir haben nun zwei Geraden: Die erste Gerade geht durch die beiden Schnittpunkte der Kreise und die zweite Gerade verbindet $P$ und $P'$. An der Stelle, an der sich diese beiden Geraden schneiden, liegt der Spiegelpunkt ($S$). Hier wurde der Spiegelpunkt grün markiert.
Vorgehensweise
Methode
Methode
- Jeweils einen Kreis um die beiden Punkte zeichnen. Diese beiden Kreise müssen den gleichen Radius haben, der so groß sein muss, dass sich die beiden Kreise schneiden.
- Durch die Schnittpunkte der beiden Kreise wird eine Gerade gezogen.
- Eine weitere Gerade wird durch den Punkt $P$ und den gespiegelten Punkt $P'$ gezogen.
- Der Schnittpunkt der beiden Geraden ist der gesuchte Spiegelpunkt $S$.
Die Spiegelachse finden
Wie können wir die Spiegelachse zwischen einem Punkt $P$ und seinem Bildpunkt $P'$ finden?
Wir beginnen wie bei der Punktspiegelung und zeichnen je einen Kreis um $P$ und $P'$.
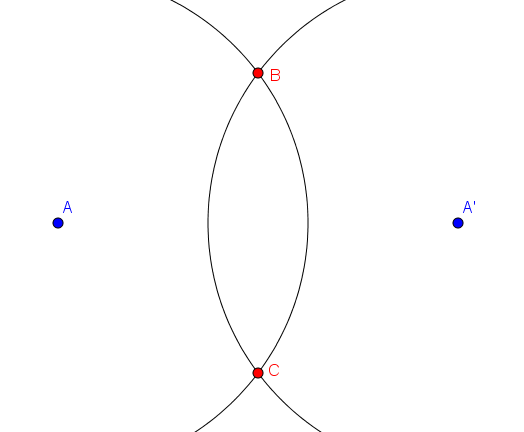
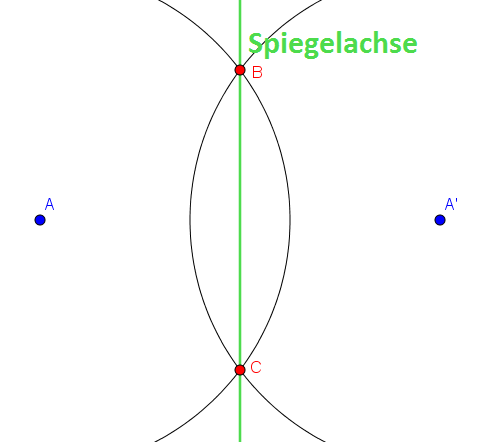
Wir sehen, dass sich die beiden Kreise im Punkt $B$ und $C$ schneiden. Durch diese beiden Punkte ziehen wir nun wieder eine Gerade. Diese Gerade ist die gesuchte Spiegelachse!
Vorgehensweise
Methode
Methode
- Jeweils einen Kreis um die beiden Punkte zeichnen. Diese beiden Kreise müssen den gleichen Radius haben, der so groß sein muss, dass sich die beiden Kreise schneiden.
- Durch die Schnittpunkte der beiden Kreise wird eine Gerade gezogen. Diese Gerade ist die Spiegelachse!
Mit den Übungsaufgaben kannst du überprüfen, ob du alles richtig verstanden hast. Viel Erfolg dabei!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
