Unterscheidung Achsen- und Punktspiegelung
In diesem Text zeigen wir dir, wie du entscheiden kannst, ob eine Figur an einem Punkt oder einer Achse gespiegelt wurde.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Entscheidungshilfen
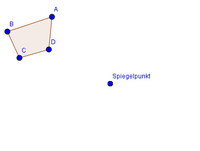
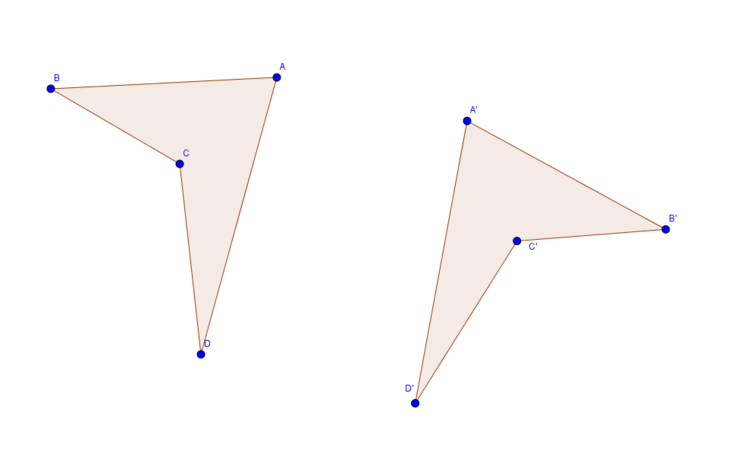
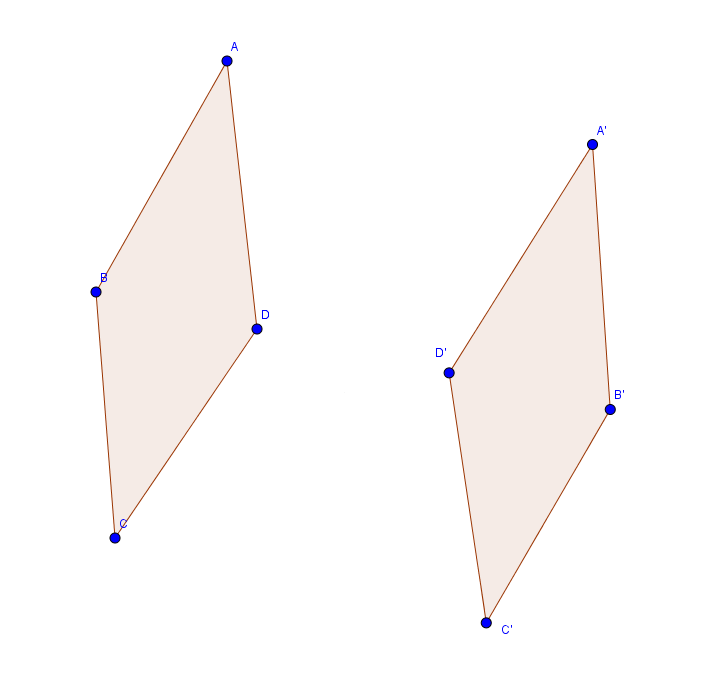
Es kann sein, dass du eine Figur und dessen Spiegelung gegeben hast und bestimmen sollst, ob dieser an einer Achse oder an einem Punkt gespiegelt wurde. Dabei gibt es ein paar Regeln, mit denen du dies ganz einfach herausfinden kannst. Schauen wir uns einen Körper an, der sowohl an einem Punkt als auch an einer Achse gespiegelt wurde.
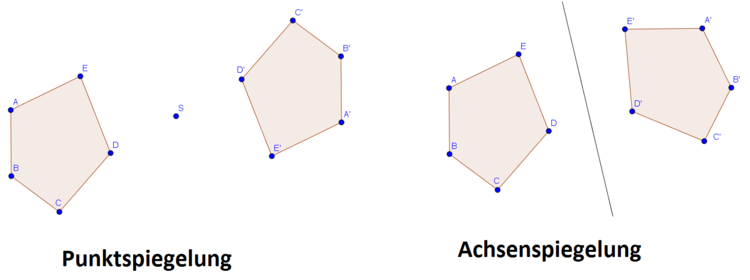
| Punktspiegelung | Achsenspiegelung | |
| Deckungsgleichheit | Körper sind deckungsgleich | Körper sind nicht deckungsgleich, sondern sie liegen aufeinander wenn an der Achse gefaltet wird |
| Richtungssinn der Buchstaben | wird beibehalten | wird vertauscht |
| Verbindung zweier Punkte $\rightarrow$ Kreuzung oder Parallelen | Geraden zwischen Punkt $A$ und $A'$ und zwischen $B$ und $B'$ schneiden sich im Spiegelpunkt | Geraden zwischen Punkt $A$ und $A'$ und zwischen $B$ und $B'$ liegen parallel zueinander |
Deckungsgleichheit
Ein Körper, der an einem Punkt gespiegelt wurde, kann so gedreht und verschoben werden, dass er auf dem Ursprungskörper liegt.
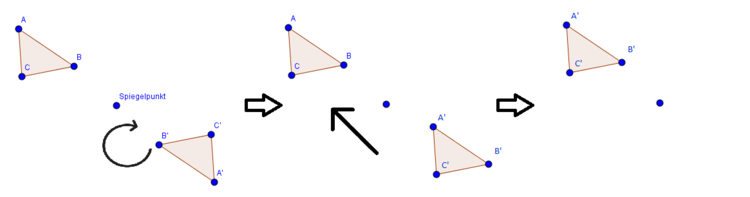
Bei einem Dreieck, welches an einer Achse gespiegelt wurde, ist dies nicht möglich.
Richtungssinn der Buchstaben
Die Eckpunkte eines Körpers werden normalerweise mit Großbuchstaben ($A$, $B$, $C$, ...) bezeichnet. Diese sind entgegengesetzt dem Uhrzeigersinn angeordnet. Wenn ein Körper nun an einem Punkt gespiegelt wurde, bleiben die Eckpunkte mit Buchstaben gegen den Uhrzeigersinn angeordnet. Wird der Körper jedoch an einer Achse gespiegelt, dreht sich die Richtung um - die Buchstabenreihenfolge steht im Uhrzeigersinn.
Verbindung zweier Punkte
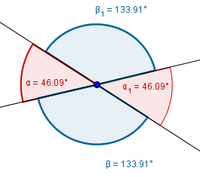
Um den letzten Punkt (Verbindung zweier Punkte $\rightarrow$ Kreuzung oder Parallelen) zu verdeutlichen, hier eine Abbildung:
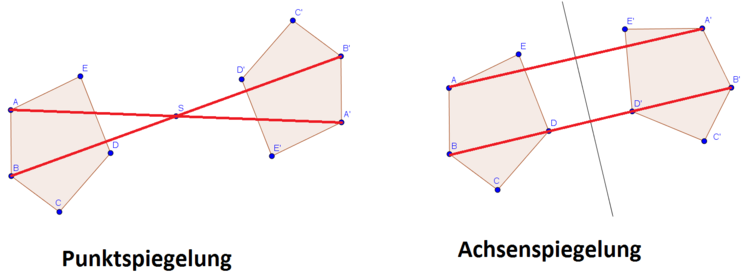
Wir sehen, dass sich die beiden Linien bei der Punktspiegelung im Spiegelpunkt schneiden. Bei der Achsenspiegelung liegen die beiden Geraden parallel zueinander.
Beispielaufgabe Spiegelung
Schauen wir uns eine Beispielaufgabe an:
Beispiel
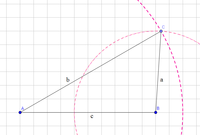
Die nachfolgende Abbildung ist gegeben und du sollst bestimmen, ob das Dreieck an einem Punkt oder einer Spiegelachse gespiegelt wurde.
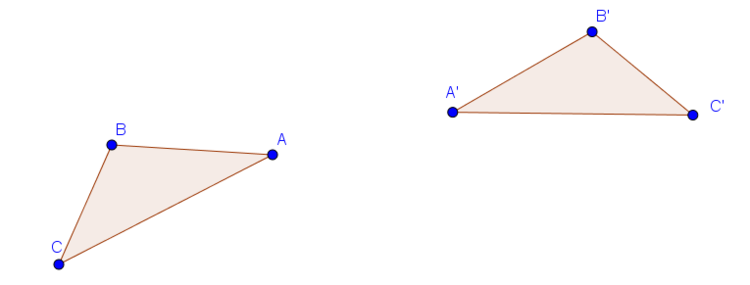
- Deckungsgleichheit
Wenn wir uns vorstellen, das Dreieck zu drehen und nach oben zu schieben, sehen wir, dass die beiden Dreiecke nicht deckungsgleich sind. Daraus lässt sich schließen, dass es an einer Achse gespiegelt wurde. - Richtungssinn der Buchstaben
Der Richtungssinn der Buchstaben ist beim Dreieck ABC gegen den Uhrzeigersinn und im gespiegelten Dreieck A'B'C' im Uhrzeigersinn. Also wurde der Richtungssinn vertauscht $\rightarrow$ Achsenspiegelung. - Verbindung der Punkte $\rightarrow$ Kreuzung oder Parallelen
Stellen wir uns vor, zwischen $A$ und $A'$ und zwischen $B$ und $B'$ sei eine Verbindungslinie. Die beiden Linien stehen parallel zueinander. Damit können wir sicher davon ausgehen, dass das Dreieck an einer Spiegelachse gespiegelt wurde!
Mit den Übungsaufgaben kannst du überprüfen, ob du alles richtig verstanden hast. Viel Erfolg dabei!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema