Begriffssammlung Mathematik 7. Klasse

Die rationalen Zahlen sind eine Erweiterung der ganzen Zahlen.

Das Symbol der rationalen Zahlen ist das $\mathbb{Q}$.

Rationale Zahlen sind alle Zahlen, die durch den Bruch zweier ganzer Zahlen dargestellt werden können. 

Man nennt rationale Zahlen in der Schule auch Bruchzahlen.

Die obere Zahl auf dem Bruchstrich wird Zähler genannt, die untere Nenner.

Zahlen mit sich wiederholenden und unendlich vielen Nachkommastellen werden mit einem Strich über den Zahlen gekennzeichnet.

Gemischte Brüche zeigen den ganzteiligen Anteil und den "Restbruch".

Subtraktion

Regel 1: Die Subtraktion zweier positiver Zahlen bleibt eine Subtraktion.

Regel 2: Die Subtraktion einer negativen Zahl von einer positiven Zahl führt zu einer Addition zweier positiver Zahlen.

Regel 3: Die Subtraktion einer positiven Zahl von einer negativen Zahl bleibt eine Subtraktion.

Regel 4: Die Subtraktion zweier negativer Zahlen führt zu einer Addition der negativen Zahl mit einer positiven Zahl.

Addition

Regel 1: Die Addition zweier positiver Zahlen bleibt eine Addition.

Regel 2: Die Addition einer negativen Zahl mit einer positiven Zahl führt zu einer Subtraktion, bei der die negative Zahl von der Positiven abgezogen wird.

Regel 3: Die Addition zweier negativer Zahlen führt zu einer Addition der beiden Zahlen unter Beibehaltung des negativen Vorzeichens beim Ergebnis.

Regel 1: "Plus mal Plus gleich Plus"

Die Multiplikation zweier positiver Zahlen ergibt eine positive Zahl.

Regel 2: "Minus mal Plus gleich Minus"

Die Multiplikation einer negativen Zahl mit einer positiven Zahl ergibt eine negative Zahl.

Regel 3: "Plus mal Minus gleich Minus"

Die Multiplikation einer negativen Zahl mit einer positiven Zahl ergibt eine negative Zahl.

Regel 4: "Minus mal Minus gleich Plus"

Die Multiplikation zweier negativer Zahlen ergibt eine positive Zahl.

Eine Division durch NULL ist nicht möglich!

Regel 1: "Plus durch Plus gleich Plus"

Die Division zweier positiver Zahlen ergibt eine positive Zahl.

Regel 2: "Minus durch Plus gleich Minus"

Die Division einer negativen Zahl mit einer positiven Zahl ergibt eine negative Zahl.

Regel 3: "Plus durch Minus gleich Minus"

Die Division einer negativen Zahl mit einer positiven Zahl ergibt eine negative Zahl.

Regel 4: "Minus durch Minus gleich Plus"

Die Division zweier negativer Zahlen ergibt eine positive Zahl.

Division = Multiplikation mit dem Kehrwert.

Um zwei rationale Zahlen zu dividieren kann man auch mit dem Kehrwert multiplizieren.

Den Kehrwert bildet man durch das Vertauschen von Zähler und Nenner.

Brüche können eliminiert werden, indem man die Gleichung mit dem Nenner multipliziert.

Schritte zum Lösen einer Bruchgleichung

• Definitionsmenge bestimmen

• Bruch lösen

• Lineare Gleichung lösen

• Überprüfung des Ergebnisses

Bei Bruchungleichungen werden Zähler und Nenner gesondert betrachtet.

Schritte zum Lösen von Bruchgleichungen mit zwei Brüchen

• Brüche auf eine Seite bringen

• Brüche zusammenfassen

• Bruchgleichung ausrechnen

Eine Gleichung besteht aus zwei Termen, die durch ein Gleichheitszeichen verbunden sind.

Deine Aufgabe ist es, die Gleichung zu lösen, d.h. für die Variable $x$ eine Zahl zu finden, mit der beide Terme denselben Wert annehmen.

Um eine Gleichung zu lösen, wendet man die Äquivalenzumformung an. Dabei gilt:

• Du musst auf beiden Seiten der Gleichung dieselbe Zahl addieren oder subtrahieren.

• Du musst auf beiden Seiten der Gleichung dieselbe Zahl (außer Null) multiplizieren oder dividieren.

Beim Lösen von Gleichungen, in denen die Variable mehrmals vorkommt, gelten folgende Arbeitsschritte:

1. Fasse die einzelnen Terme soweit wie möglich zusammen.
2. Bringe die Variable durch Äquivalenzumformung auf eine Seite.
3. Löse die Gleichung durch weitere Äquivalenzumformungen.

Eine Ungleichung beschreibt zwei Terme, die ungleich zueinander sind und verbindet diese mit ≤ und ≥ oder < und >. 

Beim Lösen einer Ungleichung erhältst du kein eindeutiges Ergebnis für $x$, sondern lediglich die Angabe, dass $x$ kleiner oder größer als eine bestimmte Zahl ist.

Ungleichungen lassen sich genauso wie Gleichungen durch Äquivalenzumformungen lösen.

Teilt man eine Ungleichung durch eine negative Zahl, muss das Größer-Kleiner-Zeichen umgedreht werden.

Kartesisches Koordinatensystem

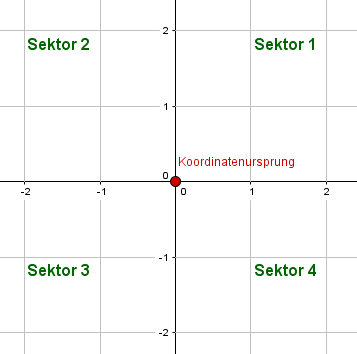
Laut Definition ist ein kartesisches Koordinatensystem ein orthogonales Koordinatensystem, dessen Koordinatenlinien in einem konstanten Abstand liegen.

Der Schnittpunkt der beiden Geraden wird der Koordinatenursprung genannt und hat den Wert (0|0).

Die x-Achse wird die waagerechte Gerade genannt, y-Achse die senkrechte Gerade.

Sektoren werden die einzelnen Bereiche des Koordinatensystems genannt. Hierbei wird rechts oben angefangen mit Sektor 1 und gegen den Uhrzeigersinn gezählt, bis man zu Sektor 4 angekommen ist.

Wertetabellen sind Tabellen, in denen x und y-Koordinaten von Punkten einer Funktion eingetragen sind. Mithilfe der Wertetabelle kann man die Funktion genau zeichnen.

Schlüsselwörter, die Verhältnisse angeben: 

...das Verhältnis zwischen... und ... ist ...

...auf XYZ kommen ABC ...

Es gibt verschiedene Schreibweisen, um ein Verhältnis zwischen zwei oder mehr Werten anzugeben. Du kannst:

...einen Bruch schreiben: $\frac {4}{1}$

...mit Doppelpunkt trennen: $4:1$

...mit einem Querstrich trennen: $4/1$

...oder mit dem Wort zu verbinden: $ 4 \; zu \; 1$

Bei proportionalen Zusammenhängen werden auf beiden Seiten der Gleichung dieselben Rechenregeln angewandt. Es gilt die Aussage: "Je mehr, desto mehr."

Bei antiproportionalen Zusammenhängen werden auf beiden Seiten der Gleichung gegensätzliche Rechenregeln angewandt. Es gilt die Aussage: "Je mehr, desto weniger."

Dreisatz aufstellen und berechnen:

1. Zusammenhang ermitteln.

2. Verhältnisse aufstellen.

3. Verhältnisse mathematisch lösen.

Jede zweidimensionale Figur ist auch gleichzeitig eine Fläche.

Viereck

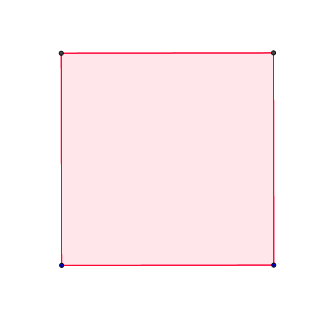
Eigenschaften von allen Vierecken:

Vierecke haben vier Linien, die vier Ecken miteinander verbinden.

Die vier Ecken werden Punkte genannt und alphabetisch benannt.

Die Seiten werden auch alphabetisch benannt. Die Namen werden hierbei klein geschrieben, um eine Verwechslung mit den Punkten zu vermeiden.

Der Quader besteht aus drei verschiedenen Seiten.

Die Länge bezeichnet die waagerechten Seiten.

Die Höhe bezeichnet die senkrechten Seiten.

Die Breite bezeichnet alle Seiten, die nach "hinten" verlaufen.

Eine Raute ist ein ebenes Viereck mit gleich langen Seiten. Die gegenüberliegenden Seiten sind parallel und gegenüberliegende Winkel sind gleich groß.