Rechtecke und Quadrate: Umfang und Flächeninhalt berechnen
Sowohl Rechtecke als auch Quadrate zählen zur Gruppe der Vierecke. Sie unterscheiden sich aber in den Kantenlängen. Bei einem Quadrat sind alle vier Seiten gleich lang. Bei einem Rechteck sind nur die gegenüberliegenden Flächen gleich lang. Am besten lässt sich dieser Unterschied anhand einer Abbildung erklären:
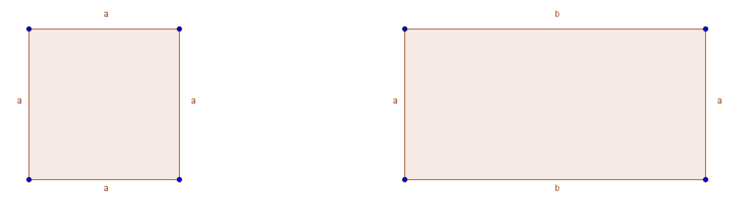
Ein Quadrat ist also eine besondere Form des Rechtecks, bei dem gilt $a=b$.
Flächeninhalt von Rechtecken
Die Flächenberechnung funktioniert bei beiden Figuren gleich und kann sowohl geometrisch als auch rechnerisch erfolgen. Bestimmen wir den Flächeninhalt zunächst über die geometrische Methode. Dabei setzen wir das Rechteck auf ein Raster aus einzelnen Quadratzentimetern und addieren die Felder. Jedes einzelne dieser Kästchen ist also 1 cm hoch und lang. Dies würde genauso gut in deinem karierten Matheheft funktionieren. Beachte aber dabei, dass ein Kästchen nicht, wie in diesem Beispiel, einem Quadratzentimeter ($1cm^2$) entspricht, sondern in der Regel $0,25 cm^2$.
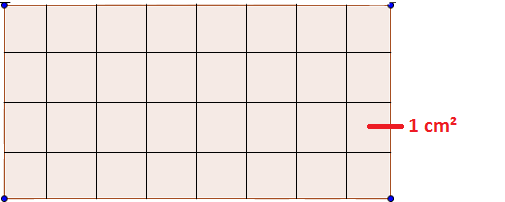
Zählen wir nun gemeinsam alle einzelnen Kästchen, erhalten wir 8 Kästchen in einer Reihe. Insgesamt liegen vier solcher Reihen aufeinander, wodurch wir auf insgesamt 32 Kästchen kommen. Die Umrechnung auf Quadratzentimeter ist in diesem Fall sehr einfach: wir erhalten $32 cm^2$.
Bei einfachen Rechtecken lässt sich diese Methode sehr gut anwenden. Um aber auch bei größeren Figuren zu einem Ergebnis zu kommen, ohne die einzelnen Quadratzentimeter zählen und addieren zu müssen, gibt es eine sehr einfache, rechnerische Methode, mit der man den Flächeninhalt berechnen kann. Wir haben gesagt, dass jedes einzelne Kästchen eine Kantenlänge von $1 cm$ hat. Die lange, untere Seite muss also 8 cm lang sein. Die Höhe des Rechtecks sind 4 Kästchen, also $4 cm$. Multipliziere ich nun die beiden Kantenlängen miteinander, erhalte ich den Flächeninhalt:
$8 cm \cdot 4 cm = 32cm^2$
Merke
Der Flächeninhalt $A$ eines Rechteckes ergibt sich aus dem Produkt seiner Seitenlängen:
$A=a \cdot b$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Umfang von Rechtecken
Eine zweite Größe, die man bei Figuren berechnen kann, ist der Umfang. Bei Rechtecken und Quadraten ist auch dies denkbar einfach. Du addierst einfach alle Kantenlängen miteinander. Für das oben gezeigte Rechteck lässt sich also folgender Umfang berechnen:
$U(=Umfang) = 8cm + 4cm +8cm +4cm$
Merke
Der Umfang $U$ eines Rechteckes ergibt sich aus der Addition der Seitenlängen:
$U= 2 \cdot (a + b)$
Flächeninhalt und Umfang bei Quadraten
Bei Quadraten funktionieren diese Rechnungen genauso, nur dass alle Längen gleich sind.
Der Flächeninhalt $A$ eines Quadrats errechnet sich auch aus dem Produkt der Seitenlängen:
$A=a \cdot a = a^2$
Für den Umfang $U$ eines Quadrats gilt: $U=4\cdot a$
Die simplen Berechnungen für Flächeninhalt und Umfang bei Rechtecken werden wir in den folgenden Beispielen immer wieder benutzen. Bei komplizierteren Formen geht man in der Regel so vor, dass man die Figur in Rechtecke zerlegt, um möglichst einfach auf ein Ergebnis zu kommen.
Rechteck berechnen: Beispiel
Führen wir nun eine Beispielrechnung durch. Versuche die Lösung zunächst selbst zu bestimmen und schau sie dir dann hier an.
Berechne nun den Umfang (U) und den Flächeninhalt (A) eines Rechtecks. Die Seitenlängen sind dabei $a=6 cm$ und $b=3 cm$
Beginnen wir mit der Berechnung des Umfangs unseres Rechtecks. Gemäß der Formel, die du ja schon kennengelernt hast, berechnest du den Umfang mit: $2\cdot (a+b)$. Setzen wir in diese Formel nun unsere Werte für a (6 cm) und b (3 cm) ein und du erhältst $U= 2\cdot (6cm+3cm)$. Wenn wir das ausrechnen, bekommen wir $2 \cdot 9cm$ und das ergibt $18cm$. Der Umfang beträgt also $U = 18 cm$.
Als nächstes wollen wir uns mit der Berechnung der Fläche auseinandersetzen. Wir nehmen die bekannte Formel ( A = a $\cdot$ b) und setzen auch hier unsere Werte ein: $A = 6cm\cdot 3cm$. Du erhältst den Flächeninhalt $A = 18 cm^2$. Bist du auf die gleichen Lösungen gekommen?
Teste und vertiefe dein neues Wissen jetzt auch in den Übungsaufgaben! Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Berechne Flächeninhalt und Umfang des Rechtecks über die geometrische und/oder die rechnerische Methode. Ein Kästchen entspricht einem Quadratzentimeter.
Welche Aussagen über das Rechteck sind korrekt? Markiere die richtigen Antworten.
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
