Kartesisches Koordinatensystem
In diesem Text erfährst du alles über das kartesische Koordinatensystem, seine Quadranten, woher der Name kommt, wie man es richtig zeichnet und die wichtigsten Begrifflichkeiten rund um das kartesische Koordinatensystem. Zudem gibt es noch ein paar Aufgaben zum Koordinatensystem, um dein Wissen zu festigen.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Begriff des kartesischen Koordinatensystems und historischer Hintergrund
Der Begriff kartesisch lässt sich von seinem Erfinder ableiten. Der Franzose René Descartes hat es im 17. Jahrhundert entwickelt und seinen Namen dafür gegeben (kartesisch ist der lateinische Begriff für Descartes).
Kartesisches Koordinatensystem: Definition und Eigenschaften
Merke
Laut Definition ist ein kartesisches Koordinatensystem ein orthogonales Koordinatensystem, dessen Koordinatenlinien in einem konstanten Abstand liegen.
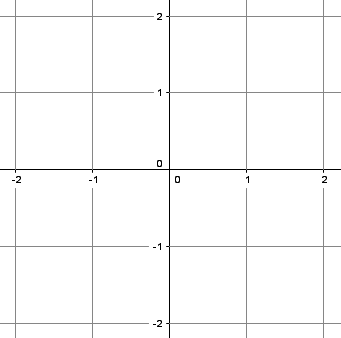
In der Abbildung erkennst du ein kartesisches Koordinatensystem. Hierbei werden zwei Geraden gezeichnet, die orthogonal aufeinander liegen, also senkrecht aufeinander. Man gibt den beiden Geraden dann im Koordinatensystem die Namen x-Achse und y-Achse, wobei die x-Achse immer die waagerechte Achse des Systems darstellt und die y-Achse immer die senkrechte Achse des Koordinatensystems ist.
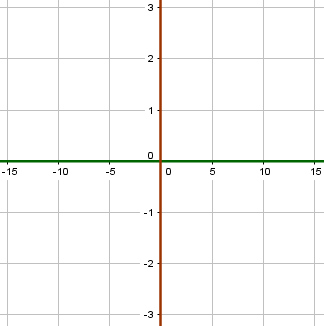
Koordinatenursprung
Den beiden Achsen werden dann bestimmte Werte in bestimmten Abständen zugewiesen, also wird etwa für jeden $cm$ im Heft genau $1 cm$ im Koordinatensystem gegangen. Man kann auch größere oder kleinere Schritte gehen, je nachdem wie man es benötigt. So haben wir in der Abbildung etwa eine Schrittgröße von 5 für die x-Achse gewählt.
Alle Koordinatensysteme haben jedoch eins gemeinsam: den Koordinatenursprung. Dieser ist der Schnittpunkt der beiden Achsen und hat immer die Koordinaten (0|0).
Merke
Der Schnittpunkt der beiden Geraden wird der Koordinatenursprung genannt und hat den Wert (0|0).
Die x-Achse wird die waagerechte Gerade genannt, y-Achse die senkrechte Gerade.
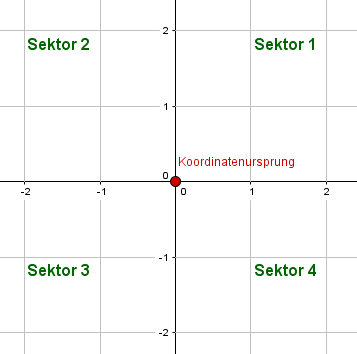
Quadranten im Koordinatensystem
Wie wir in der Abbildung erkennen, werden die einzelnen Bereiche in einem Koordinatensystem auch mit einem bestimmten Namen versehen. Wir nennen den rechten oberen Bereich Sektor 1, 1. Sektor oder 1. Quadrant. Der 2. Sektor bzw. 2. Quadrant ist dann der links daneben, der dritte der darunter und der vierte der letzte verbleibende Bereich. So hat jeder Bereich seinen bestimmten Namen. Die Sektoren bzw. Quadranten im Koordinatensystem erleichtern das Eintragen und Ablesen von Punkten.
Merke
Die einzelnen Bereiche des Koordinatensystems werden Quadranten/Sektoren genannt. Hierbei wird rechts oben angefangen mit Quadrant 1 und gegen den Uhrzeigersinn gezählt bis man zu Quadrant 4 angekommen ist.
Gut zu wissen
Manchmal wirst du bei Koordinatensystemen statt des Begriffs Quadrant, auch den Begriff Sektor finden. Dieser ist ebenfalls richtig, Quadrant ist nur der lateinischen Sprache entnommen. Es bedeutet so viel wie Viertel. Du kannst also beide Begriffe verwenden.
Kartesisches Koordinatensystem: Punkte ablesen und eintragen
Wie liest man also Punkte in einem Koordinatensystem ab oder trägt diese ein?
Nehmen wir als Beispiel den Punkt P(2|3). Wir haben zwei Koordinaten gegeben, einmal die $\textcolor{blue}{2}$ und einmal die $\textcolor{green}{3}$. Der erste der beiden Werte ist der $\textcolor{blue}{x-Wert}$, also ist der andere der $\textcolor{green}{y-Wert}$. Wenn wir also das Koordinatensystem vor uns haben gehen wir erst die Schritte auf der x-Achse, hier genau 2. Die Schritte gehen wir in Richtung des 1.Sektors, weil die Zahl 2 positiv ist. Wenn sie negativ wäre, müsste man Richtung Sektor 2 gehen.
Jetzt gehen wir nur noch die Schritte in die richtige Richtung für den y-Wert. Hier also 3 Schritte, die wir nach oben gehen, da die y-Achse nach oben hin die positiven Werte hat. In einer Abbildung sieht das dann so aus:
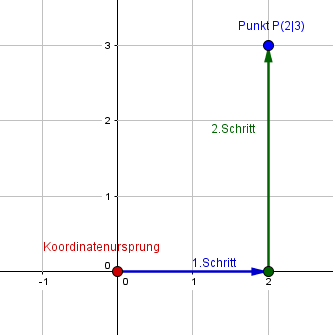
Die blaue und die grüne Linie sind natürlich nur Hilfslinien, die du nicht einzeichnen musst, wenn du den Punkt in dein Koordinatensystem einträgst.
Wenn du einen Punkt ablesen willst, gehst du fast genauso vor. Du schaust erst nach der x-Achse und gehst die Schritte, bis du unter dem Punkt gelandet bist (oder über dem Punkt wenn der y-Wert negativ ist). Dann gehst du die Schritte zum Punkt. Wenn du dir beide Werte gemerkt hast, dann hast du jetzt die Koordinaten des Punktes herausgefunden.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen zum kartesischen Koordinatensystem!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
