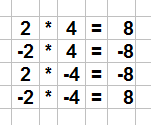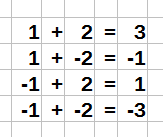Multiplizieren und Dividieren rationaler Zahlen - so funktioniert's
Das Multiplizieren und Dividieren von natürlichen Zahlen hast du bereits gelernt. Doch mit der Einführung der rationalen Zahlen kommen auch neue Schwierigkeiten hinzu. In diesem Kapitel widmen wir uns der Multiplikation und der Division von rationalen Zahlen und erklären dir die wichtigsten Regeln.
Rationale Zahlen
Merke
Mit rationalen Zahlen sind alle Zahlen gemeint, die durch ein Verhältnis zweier ganzer Zahlen dargestellt werden können.
Ihr Symbol ist das $\mathbb Q$.
Multiplikation rationaler Zahlen - Regeln
Bisher hast du die Multiplikation von ganzen Zahlen kennengelernt. Die vier Regeln zur Multiplikation gelten auch bei den rationalen Zahlen. In der folgenden Abbildung sind die vier Regeln noch einmal dargestellt:
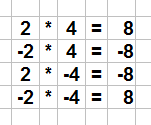
Merke
Regel 1: "Plus mal Plus gleich Plus"
Die Multiplikation zweier positiver Zahlen ergibt eine positive Zahl.
Regel 2: "Minus mal Plus gleich Minus"
Die Multiplikation einer negativen Zahl mit einer positiven Zahl ergibt eine negative Zahl.
Regel 3: "Plus mal Minus gleich Minus"
Die Multiplikation einer negativen Zahl mit einer positiven Zahl ergibt eine negative Zahl.
Regel 4: "Minus mal Minus gleich Plus"
Die Multiplikation zweier negativer Zahlen ergibt eine positive Zahl.
Die Abbildung und die Merkebox zeigen uns die besondere vierte Regel. Diese besagt, dass bei der Multiplikation zweier negativer Zahlen eine positive Zahl die Lösung ist. Das folgende Beispiel zeigt uns das genauer:
Multiplikation rationaler Zahlen - Beispiel
Beispiel
Wir haben die beiden Brüche $\Large{(-\frac{1}{2})}$ und $\Large{(-\frac{3}{5})}$ gegeben. Diese sollen miteinander multipliziert werden. Es folgt also:
$\Large{(-\frac{1}{2}) \cdot (-\frac{3}{5})}$
Im ersten Schritt schreiben wir alles auf einen Bruchstrich. Hierbei können wir direkt die beiden Minuszeichen gegeneinander kürzen:
$\Large{\frac{1 \cdot 3}{2 \cdot 5}}$
Der zweite Schritt ist das Kürzen der Nenner und Zähler. Da dies hier nicht möglich ist, folgt direkt das Multiplizieren und als Lösung ergibt sich:
$\Large{\frac{3}{10}}$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Division rationaler Zahlen - Regeln
Merke
Eine Division durch NULL ist nicht möglich!
Die Division bei rationalen Zahlen folgt ebenso den vier Grundregeln der Division. Diese sind in der folgenden Abbildung und auch in der darunter liegenden Merkebox noch einmal dargestellt:
Merke
Regel 1: "Plus durch Plus gleich Plus"
Die Division zweier positiver Zahlen ergibt eine positive Zahl.
Regel 2: "Minus durch Plus gleich Minus"
Die Division einer negativen Zahl mit einer positiven Zahl ergibt eine negative Zahl.
Regel 3: "Plus durch Minus gleich Minus"
Die Division einer negativen Zahl mit einer positiven Zahl ergibt eine negative Zahl.
Regel 4: "Minus durch Minus gleich Plus"
Die Division zweier negativer Zahlen ergibt eine positive Zahl.
Diese vier Regeln der Division gelten auch für die rationalen Zahlen. Doch die Division von rationalen Zahlen hat eine Besonderheit:
Merke
Division = Multiplikation mit dem Kehrwert.
Du kannst, anstatt zu dividieren, auch mit dem Kehrwert multiplizieren. Wir schauen uns das an einem Beispiel an:
Division rationaler Zahlen - Beispiel
Beispiel
Wir dividieren die beiden Zahlen $\Large{\frac{18}{5}}$ und $\Large{\frac{6}{1}}$. Der Term lautet dann:
$\Large{\frac{18}{5} : \frac{6}{1}}$
Auf einem Bruch ergibt sich:
$\Large{\frac{18:6}{5:1}}$
Die Lösung ist:
$\Large{\frac{3}{5}}$
Oder wir multiplizieren mit dem Kehrwert:
$\Large{\frac{18}{5} : \frac{6}{1}}$
Der Kehrwert von $\Large{\frac{6}{1}}$ ist $\Large{\frac{1}{6}}$
$\Large{\frac{18}{5} \cdot \frac{1}{6}}$
Alles auf einen Bruch schreiben:
$\Large{\frac{18 \cdot 1}{5 \cdot 6}}$
Kürzen:
$\Large{\frac{\cancel{18}\;3 \cdot 1}{5 \cdot \cancel{6}\;1}}$
Im letzten Schritt folgt das Ausmultiplizieren:
$\Large{\frac{3}{5}}$
Merke
Um zwei rationale Zahlen zu dividieren kann man auch mit dem Kehrwert multiplizieren.
Den Kehrwert bildet man durch vertauschen von Zähler und Nenner.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
