Formelsammlung Mathematik 7. Klasse

Das Rechteck

Der Flächeninhalt $A$ eines Rechteckes ergibt sich aus dem Produkt seiner Seitenlängen:

$A=a \cdot b$.

Der Umfang $U$ eines Rechteckes ergibt sich aus der Addition der Seitenlängen:

$U= 2 \cdot (a + b)$.

Der Flächeninhalt $A$ eines Quadrats errechnet sich auch aus dem Produkt der Seitenlängen:

$A=a \cdot a = a^2$.

Der Umfang eines Quadrates ergibt sich aus der Addition der Seitenlängen. Da alle Seiten gleich lang sind, kann man den Umfang auch durch die Multiplikation der Seitenlänge mit $4$ berechnen:

 $U=4\cdot a$.

Eine allgemeine Raute

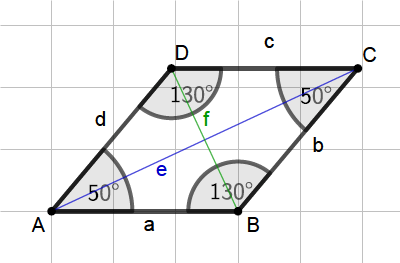
Der Flächeninhalt $A$ einer Raute errechnet sich aus der Multiplikation der beiden Diagonalen ($e,f$) dividiert durch $2$:

$A= \frac{1}{2} \cdot e \cdot f$.

Der Umfang einer Raute ist die Addition der einzelnen Seiten: $U= a + b + a + b$

Für den Fall, dass alle Seiten der Raute gleich lang sind, gilt folgende Formel:

Umfang $U= a + a + a + a$ oder $U = 4 \cdot a$.

Der Umfang $U$ eines Trapezes berechnet sich durch die Addition der Seitenlängen:

$U = a + b +c +d$.

Der Flächeninhalt eines Trapezes berechnet sich wie folgt:

$A = \frac{1}{2} \cdot (b + d) \cdot h$

Dabei entspricht $b$ der Grundseite und $d$ der Oberkante. Beachte, dass Oberkante und Grundseite in anderen Aufgaben unterschiedlich benannt sein können!

Das Parallelogramm

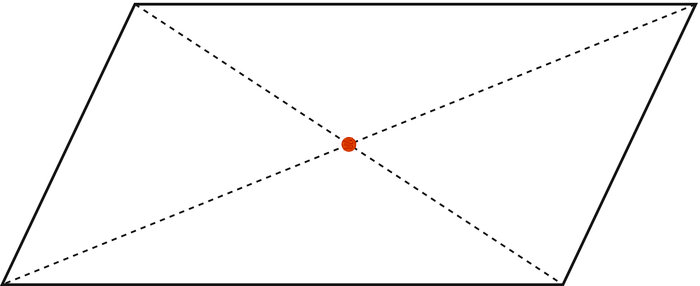
Für den Flächeninhalt $A$ eines Parallelogramms gilt:

$A= b\cdot h_{b}$.

Dabei entspricht $h_{b}$ der Höhe des Parallelogramms auf der Seite $b$.

Für den Umfang $U$ eines Parallelogramms gilt:

$U = 2\cdot (a + b)$.

Den Flächeninhalt $A$ eines Dreiecks errechnet sich aus der halben Grundseite mal der Höhe. Da nicht immer klar ist, was genau die Grundseite ist, können wir diese Regel auch allgemeiner formulieren:

$A = \frac{1}{2} \cdot (a \cdot h_{a})$

$A = \frac{1}{2} \cdot (b \cdot h_{b})$

$A = \frac{1}{2} \cdot (c \cdot h_{c})$

Der Umfang $U$ eines Dreiecks berechnet sich durch die Addition der Seitenlängen.

$U = a + b + c$.

In einem Dreieck ist die Summe der Innenwinkel immer 180° - nie weniger und nie mehr!

Innenwinkelsatz: $\alpha + \beta + \gamma = 180°$.

Der Höhenschnittpunkt $H$ ist der Schnittpunkt aller drei Höhen eines Dreiecks.

Der Inkreismittelpunkt $I$ ist der Schnittpunkt der Winkelhalbierenden eines Dreiecks.

Der Umkreismittelpunkt $U$ ist der Schnittpunkt aller drei Mittelsenkrechten eines Dreiecks.

Der Schwerpunkt $S$ ist der Schnittpunkt der Seitenhalbierenden eines Dreiecks.

Der Flächeninhalt $A$ eines rechtwinkligen Dreiecks berechnet sich aus der Hälfte des Produktes der am rechten Winkel anliegenden Seiten.

$A = \frac{1}{2} \cdot (a \cdot b)$

Der Umfang $U$ errechnet sich genauso wie bei anderen Dreiecken.