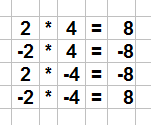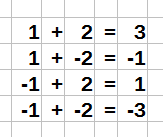Rechnen mit rationalen Zahlen
Das Addieren und Subtrahieren von natürlichen Zahlen hast du bereits gelernt. Doch mit der Einführung der rationalen Zahlen kommen auch neue Schwierigkeiten und Herausforderungen hinzu. In diesem Kapitel widmen wir uns der Addition und der Subtraktion von rationalen Zahlen und erklären dir die wichtigsten Regeln. Außerdem findest du am Ende dieses Lerntextes zum Thema Rechnen mit rationalen Zahlen Übungsaufgaben, sodass du sofort auf Online-Arbeitsblättern dein Wissen zu rationalen Zahlen vertiefen und überprüfen kannst.
Gut zu wissen
Im Lerntext Multiplizieren und Dividieren rationaler Zahlen - so funktioniert's erklären wir dir die Regeln und die Vorgehensweise, wenn du rationale Zahlen multiplizieren und dividieren musst.
Rationale Zahlen
Merke
Die rationalen Zahlen sind alle Zahlen, die durch ein Verhältnis zweier ganzer Zahlen dargestellt werden können. Vereinfacht gesagt: Alle Zahlen, die als Bruch aus ganzen Zahlen darstellbar sind, zum Beispiel $\frac{5}{2}$.
Ihr Symbol ist das $\mathbb Q$.
Besonders an den rationalen Zahlen ist, dass unendlich viele rationale Zahlen zwischen zwei ganzen Zahlen liegen. Du kannst dir auch Folgendes über die rationalen Zahlen merken:
- Jede natürliche Zahl ist eine rationale Zahl, zum Beispiel $13$.
- Jede ganze Zahl ist eine rationale Zahl, zum Beispiel $-5$.
- Jede positive rationale Zahl ist eine rationale Zahl, zum Beispiel $7,9$.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Rationale Zahlen addieren - Regeln
Bei der Addition rationaler Zahlen gibt es verschiedene Möglichkeiten, wie du rechnen kannst. So rechnest du nicht nur mit positiven Zahlen, sondern auch mit negativen Zahlen oder sogar Brüchen. Für die Addition solcher rationaler Zahlen gibt es vier Regeln:
In der Abbildung siehst du die vier Regeln zur Addition rationaler Zahlen. Die erste Regel sollte dir bekannt sein:
Merke
Regel 1:
Wenn zwei positive Zahlen addiert werden, ergibt sich dabei eine positive Zahl.
Die zweite Regel ist eine der interessanteren Regeln. Wenn wir zu einer positiven Zahl eine negative Zahl addieren wollen, wird aus der Addition eine Subtraktion.
Aus der Addition: $1 \; + \; (-2)$
entsteht folgendes: $1 \; - \; 2$.
Das liegt daran, dass das Minuszeichen vor der $(-2)$ mit dem $+$ verrechnet wird und es entsteht ein Minuszeichen. Man kann also umgangssprachlich sagen, dass das Minuszeichen einen höheren Wert als das Pluszeichen hat und jedes Mal, wenn du eine negative Zahl addieren willst, eine Subtraktion entsteht.
Merke
Regel 2:
Wird zu einer positiven Zahl eine negative Zahl addiert, ergibt sich eine Subtraktion.
Die dritte Regel sollte dir auch schon von der Addition ganzer Zahlen bekannt sein. Denn die Addition einer positiven Zahl und einer negativen Zahl ist eine ganz gewöhnliche Addition.
Merke
Regel 3:
Addiert man zu einer negativen Zahl eine positive Zahl gibt es keine Besonderheiten. Es bleibt bei einer Addition.
Die vierte und letzte Regel der Addition ist wieder etwas interessanter. Hierbei wird zu einer negativen Zahl eine negative Zahl addiert. Das Beispiel lautet: $(-1) \; + \; (-2)$.
Genauso wie bei Regel 2 entsteht eine Subtraktion: $ (-1) \; - \; 2$.
Merke
Regel 4:
Bei der Addition zweier negativer Zahlen ergibt sich eine Subtraktion beider Zahlen.
Rationale Zahlen subtrahieren - Regeln
Auch bei der Subtraktion gibt es bei solchen rationalen Zahlen vier Regeln. In der Abbildung sehen wir sie genauer:
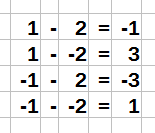
Die interessanteste der Regeln ist hier die Regel 2. Wir sehen, dass sie Subtraktion einer negativen Zahl zu einer Addition führt. Man kann auch umgangssprachlich sagen: "Minus auf Minus ergibt Plus".
Merke
Regel 1: Die Subtraktion zweier positiver Zahlen bleibt eine Subtraktion.
Regel 2: Die Subtraktion einer negativen Zahl von einer positiven Zahl führt zu einer Addition zweier positiver Zahlen.
Regel 3: Die Subtraktion einer positiven Zahl von einer negativen Zahl bleibt eine Subtraktion.
Regel 4: Die Subtraktion zweier negativer Zahlen führt zu einer Addition der negativen Zahl mit einer positiven Zahl.
Nun weißt du schon einmal mehr darüber, wie du rationale Zahlen addieren und subtrahieren kannst. Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
